Níže uvedené úlohy jsou uvedeny jako ukázkové s úplným řešením. Po projití těchto úloh bude ještě následovat Sada úloh k samostatnému řešení, u těchto úloh jsou už uvedeny pouze výsledky. Dále je možno pokračovat Užitím integrálního počtu ve fyzice, kde jsou odkazy na studijní texty z FO.
| a) Obsah rovinného
obrazce Je-li funkce f spojitá a nezáporná na intervalu áa, bñ, je obsah S množiny na obrázku vpravo určen vztahem
|
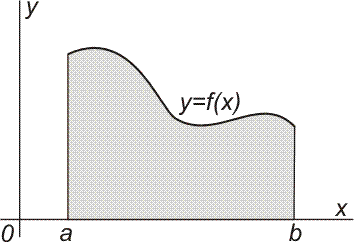 |
| Jsou-li
funkce f, g spojité na intervalu
áa,
bña
je-li f(x) ≤ g(x) pro všechna x
Î áa,
bñ,
je obsah S množiny, vyšrafované na obrázku vpravo, určen vztahem
|
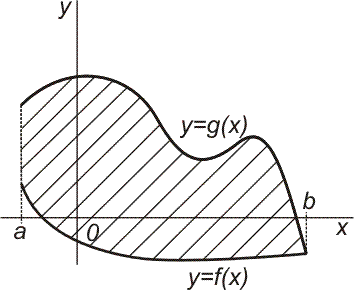 |
| b) Objem rotačního tělesa Je-li funkce y = f(x) spojitá a nezáporná na intervalu áa, bñ, je objem rotačního tělesa vzniklého rotací křivky f(x) kolem osy x (obrázek vpravo) určen vztahem
|
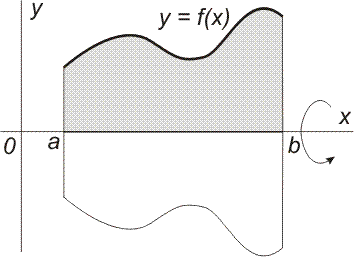 |
| c) Obsah rotační
plochy Má-li funkce y = f(x) spojitou derivaci na intervalu áa, bñ a je-li v tomto intervalu nezáporná, je obsah rotační plochy vzniklé rotací grafu funkce f(x) kolem osy x určen vztahem
d) Délka křivky Nechť je funkce y = f(x) spojitá na intervalu áa, bñ a nechť má na intervalu áa, bñ spojitou a neomezenou derivaci. Délka křivky, která je jejím grafem, je pak určena vztahem
|
Užití určitého integrálu ve fyzice
a) Kinematika
Je-li a(t), kde t Î át0; t1ñ, zrychlení přímočarého pohybu v čase t, a je-li v0 rychlost pohybu v čase t0, je rychlost pohybu v(t) v čase t určena vztahem
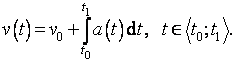
Je-li v(t), kde t Î át0; t1ñ, rychlost přímočarého pohybu v čase t a je-li s0 dráha pohybu v čase t0, je dráha s(t) v čase t určena vztahem
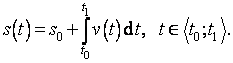
Příklad 1
Hmotný bod koná přímočarý pohyb tak, že jeho zrychlení s časem rovnoměrně roste a za prvních 10 s pohybu vzroste z nulové hodnoty na 5 m×s-2. Jaká je rychlost pohybu hmotného bodu v čase t = 10 s a jakou dráhu hmotný bod za tuto dobu urazil, jestliže v čase t = 0 s byl v klidu?
Obdobné vztahy jako pro přímočarý pohyb platí i pro pohyb hmotného bodu po kružnici, tj.
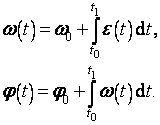
| Na element plochy
působí tlaková síla
Na celou plochu pak působí tlaková síla, která je dána součtem jednotlivých tlakových sil, tj.
|
 |
| Příklad 2 Deska D, mající tvar parabolické úseče s výškou 20 m a délkou tětivy 4 m, je zavěšena v nádrži s vodou, jak ukazuje obrázek vpravo. Hladina vody splývá s osou x. Určete velikost síly, kterou působí voda na jednu stranu desky. Uvažujte g = 10 m×s-2, ρ = 1000 kg×m-3 .
|
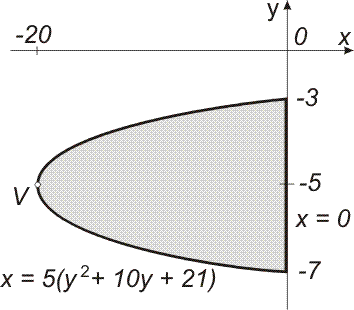 |
| Příklad 3 - síla působící na
otáčející se tyč Homogenní válcová kovová tyč o hustotě ρ = 8 g × cm-3 a délce l = 30 cm se otáčí kolem pevné osy procházející těžištěm tyče kolmo na směr délky úhlovou rychlostí ω. Jaká může být největší úhlová rychlost otáčení, jestliže největší dovolené napětí, kterému můžeme tyč v podélném směru vystavit, je σD = 60 MPa? |
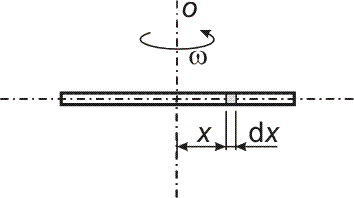 |
| Příklad 4 -
síla působící v gravitačním poli Určete velikost gravitační síly, kterou na sebe navzájem působí hmotný bod o hmotnosti m1 a homogenní tyč délky l a hmotnosti m2, jejíž hmotný střed má vzdálenost a od hmotného bodu a leží v prodloužení podélné osy tyče (viz obrázek níže). |
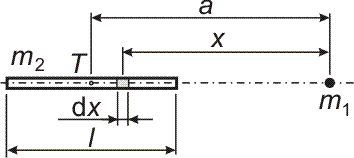 |
c) Výpočet práce
Práce síly F je dána integrálem ze skalárního součinu síly F a elementární dráhy ds. Je-li směr obou vektorů stejný, pak můžeme psát
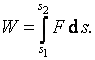
Bude-li síla F konstantní, pak
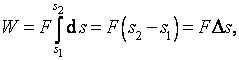
což je známý vztah.
| Příklad 5 - práce
vykonaná při čerpání nádoby Vypočtěte práci, kterou musíme vykonat, abychom vyčerpali nádrž tvaru polokoule, je-li naplněna do poloviny vodou (viz obrázek vpravo). Poloměr je r = 2 m.
|
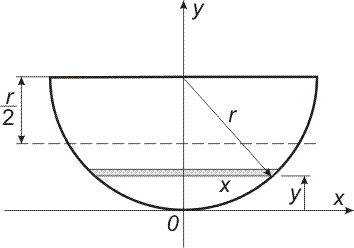 |
| Příklad 6 - práce
vykonaná v elektrostatickém poli Vypočtěte práci, kterou musíme vykonat, abychom přenesli kladný jednotkový náboj Q1 = 1 C z nekonečna do bodu A, který je od bodového náboje Q = 1000 C vzdálen o r = 1 m. |
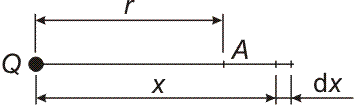 |
| Příklad 7
- potenciál gravitačního pole Odvoďte vztah pro potenciál gravitačního pole ve vzdálenosti r od hmotného bodu o hmotnosti m. |
Gravitační potenciální energie
| Newtonův gravitační zákon ve tvaru pro dva hmotné body
platí také pro dvě homogenní koule nebo koule se středově souměrně
rozloženou hustotou. Předpokládejme nyní, že jedno z těles je Země a
druhé hmotný bod. I v tomto případě platí Newtonův gravitační zákon ve
tvaru
Budeme uvažovat, že se hmotný bod přemístí z bodu A do bodu B (viz obrázek vpravo). |
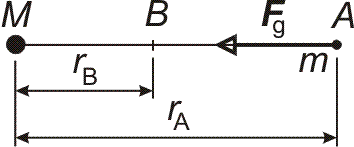 |
Určíme práci, kterou hmotný bod vykoná působením síly Fg.
Tuto práci určíme jako součet elementárních prací, tj. dW = Fg dr (Fg , dr mají stejný směr), potom
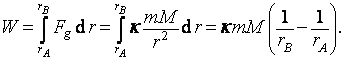
Tato práce se rovná rozdílu gravitační potenciální energie hmotného bodu v počátečním a koncovém bodě trajektorie AB; nezávisí na tvaru trajektorie hmotného bodu mezi A a B.
Tyto poznatky využijeme při řešení následující úlohy.
Příklad 8 - kinetická energie padajícího tělesa
Vypočítejte kinetickou energii Ek tělesa o hmotnosti m, volně padajícího z výšky H, při jeho dopadu na zemský povrch, jestliže poloměr Země je R. Jaká by byla tato energie, kdyby H » R? (Odpor vzduchu zanedbejte.)
Příklad 9 - práce vykonaná při prodloužení pružiny
Na pružině je zavěšeno závaží o hmotnosti m = 2 kg. Působíme-li na toto závaží silou F = 30 N svisle dolů, prodlouží se pružina o 66 cm. Určete práci síly F při prodloužení pružiny (uvažujte g = 10 ms-2).
Přeměna elektrické energie v tepelnou
Prochází-li rezistorem o konstantním odporu R elektrický proud I(t); t Î át0; t1ñ, určíme množství elektrické energie E, která se při tom přemění v tepelnou podle vztahu:
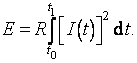
Více informací o obvodech střídavého proudu je možno získat ve studijním textu
Obvody střídavého proudu - formát PS nebo formát PDF.
Příklad 10
Vypočítejte, kolik tepelné energie vznikne při průchodu proudu I = I0 sin ωt rezistorem o odporu R = 2 Ω po dobu t Î át0; t1ñ, jestliže I0 = 20 A, ω = 314 rad × s-1, t Î á0 s; 7 sñ.
Návod: při výpočtu sestaveného integrálu použijte vztahu
![]()
Příklad 11
Vypočítejte práci střídavého proudu I = I0 sin ωt ve vodiči s rezistorem R za jednu periodu T.
Práce plynu
Při výpočtu práce ideálního plynu budeme používat následující vztahy:
1. termodynamický zákon ΔU = W + Q, který si upravíme pomocí diferenciálů na tvar dU = dQ + dW. Je-li dW (nebo dQ) záporná, soustava práci (nebo teplo) od svého okolí nepřijímá, ale odevzdává mu ji. Obvykle používáme značení dW ´ (dQ ´), koná-li práci soustava (odevzdává-li teplo svému okolí). Platí vztahy dW = - dW ´, dQ = - dQ ´.
Práce, kterou vykoná plyn při elementární změně svého objemu o dV, je dána vztahem dW´ = p dV.
Po integraci vztahu pro práci dW ´ pak můžeme psát
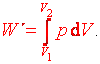
Dále budeme při výpočtech souvisejících s prací ideálního plynu používat stavovou rovnici ideálního plynu v různých tvarech, nejčastěji pak ve tvarech
![]()
Výpočet práce ideálního plynu také velmi úzce souvisí s pojmy tepelná kapacita plynu. Zde rozlišujeme tepelnou kapacitu plynu za stálého objemu Cv a tepelnou kapacitu plynu za stálého tlaku Cp. Častěji pak pracujeme s tzv. molárními tepelnými kapacitami, které jsou definovány takto:
![]()
kde Mm je molární hmotnost plynu. Připomeňme si platnost vztahu Mm = Mr × 10-3.
Jestliže se při elementární stavové změně jednoho molu ideálního plynu jeho teplota změní o dT, jeho vnitřní energie U se změní o
![]()
Uvažujeme-li plyn o hmotnosti m, pak obsahuje
![]()
takže
![]()
Vztah mezi molární tepelnou kapacitou ideálního plynu za stálého tlaku a stálého objemu vyjadřují dvě rovnice:
a) Mayerova rovnice
![]()
pro měrné tepelné kapacity cp, cv pak platí
![]()
b) Rovnice, pomocí které je definována Poissonova konstanta κ
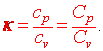
Z výše uvedených rovnic pak plyne pro Poissonovu konstantu κ vztah
![]()
Více informací o vztazích, které platí pro ideální plyn je možno získat ve studijním textu:
Kruhový děj v ideálním plynu - formát PS nebo formát PDF.
Příklad 12
Vzduch o tlaku 20 Pa je adiabaticky stlačen z 200 m3 na 50 m3. Určete výsledný tlak a velikost vykonané práce za předpokladu, že vzduch se chová jako ideální plyn.
Příklad 13
Vypočtěte, kolik tepla se musí odejmout chlazením při izotermickém stlačení m = 45 g oxidu uhličitého CO2 teploty t1 = - 15 0C a tlaku p1 = 0,23 MPa na tlak p2 = 0,58 MPa.
Příklad 14
Vzduch o objemu V0 = 10 litrů, teplotě t0 = 0 0C a tlaku p0 = 0,1 MPa nejprve izotermicky stlačíme na objem V1 = 2 litry a potom adiabaticky rozepneme na objem V2 = 20 litrů. Jaká bude výsledná teplota vzduchu po ukončení této stavové změny a jaká celková práce se při tom spotřebuje? (κ = 1,4 pro vzduch)
d) Těžiště tělesa
Ukážeme si, jak počítat polohu hmotného středu některých těles. Budeme předpokládat, že uvažované těleso je v homogenním tíhovém poli, tj. budeme mluvit o těžišti tělesa.
Připomeňme si základní podmínky pro výpočet těžiště tělesa:
Na základě těchto podmínek můžeme např. psát
![]()
odtud pak dostáváme pro souřadnice těžiště vztah
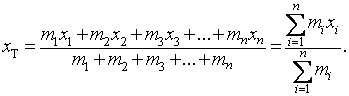
Stejné vztahy platí i pro ostatní osy
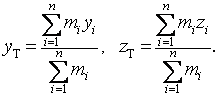
Uvažujeme-li těleso se spojitě rozloženou hmotností, pak můžeme psát
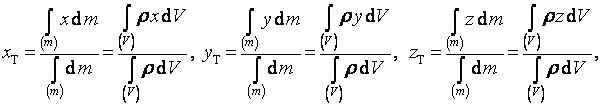
kde jsme položili dm = ρ dV, ρ je hustota tělesa, dV objemový element, dm hmotnostní element. Vztahy bychom ještě mohli upravit užitím toho, že
kde m je hmotnost tělesa.
| Příklad 15 Stanovte polohu těžiště homogenního velmi tenkého drátu kruhového oblouku s poloměrem r a středovým úhlem 2α.
|
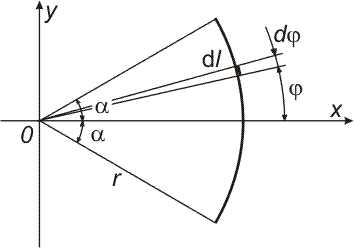 |
| Příklad 16 Určete polohu těžiště homogenního rotačního kužele výšky v a poloměru r.
|
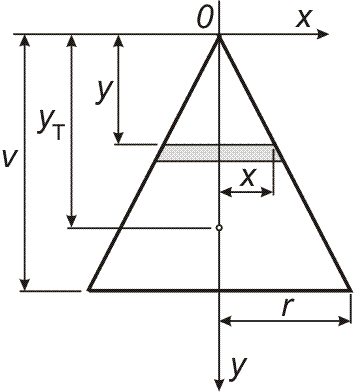 |
e) Výpočet momentu setrvačnosti
V této části si ukážeme, jak počítat moment setrvačnosti některých těles užitím integrálního počtu.
Doposud byl moment setrvačnosti J tuhého tělesa vzhledem k ose otáčení definován pomocí součtu
![]()
kde ri je vzdálenost hmotného bodu mi od osy otáčení.
U těles se spojitě rozloženou látkou platí obdobný vztah
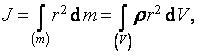
kde jsme použili vztah dm = ρ dV.
Značka (m) resp. (V) u integrálu značí, že integrujeme přes celé těleso.
Výpočet momentu setrvačnosti těles vzhledem k libovolné ose otáčení ulehčují některé věty, především Steinerova věta:
![]()
kde J0 je moment setrvačnosti vzhledem k ose procházející těžištěm, a je vzdálenost osy otáčení od osy procházející těžištěm, m je hmotnost tělesa.
| Příklad 17 Určete moment setrvačnosti homogenní tyče délky l a hmotnosti m vzhledem k ose kolmé na směr délky tyče a) procházející koncovým bodem tyče, b) procházející středem tyče. |
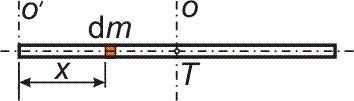 |
| Příklad 18 Určete moment setrvačnosti homogenní kruhové desky hmotnosti m = 2 kg a poloměru r = 10 cm vzhledem k ose procházející středem desky kolmo na rovinu desky.
|
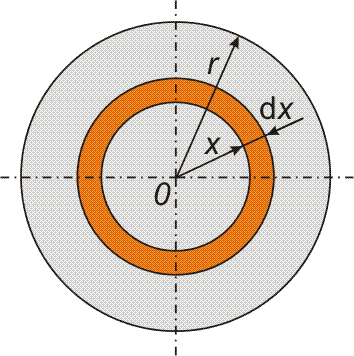 |
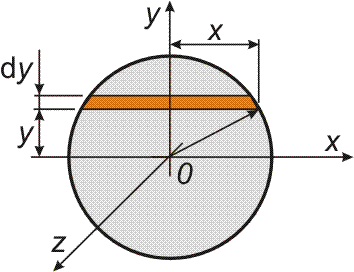
| Příklad 19 Určete moment setrvačnosti homogenní koule o poloměru r a hmotnosti m vzhledem k ose jdoucí středem koule.
|
 |
Pokračovat je nyní možno řešením sady úloh, kde jsou uvedeny pouze výsledky.