[Návrat do menu integrál]

Úlohy na procvičování

(vhodné k samostatné práci)

    Příklad 1

Jak velkou silou působí voda na boční obdélníkovou stěnu nádoby, jestliže vodorovná délka stěny a = 20 cm a svislá b = 15 cm a je-li nádoba zcela zaplněná vodou? (g = 9,81 m × s^-2, ρ = 1000 kg × m^-3)

    Výsledek

Příklad 2 Nádrž, jejímž průřezem je rovnoramenný lichoběžník, nakreslený na obrázku vpravo, je naplněna vodou. Jaká síla působí na jednu stěnu?     Výsledek

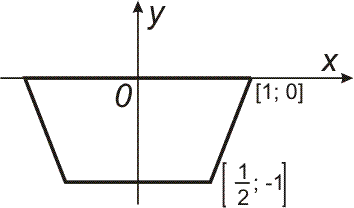Příklad 3 Rotační kuželová nádoba o výšce 10 m a poloměru 6 m (nahoře) je plná vody (viz obrázek vpravo). Kolik práce se vykoná při vypumpování celého obsahu do výše okraje nádoby?           Výsledek

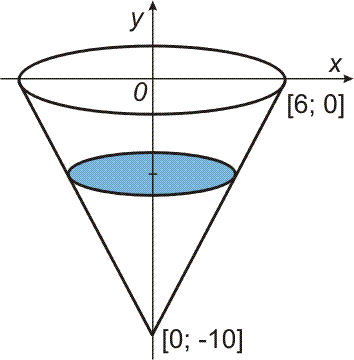     Příklad 4

Koule plave v kapalině hustoty ρ tak, že je do ní ponořená polovinou svého objemu. Jaká práce se vykoná při vytažení koule nad hladinu kapaliny, jestliže poloměr koule je R ?

     Výsledek

     Příklad 5

 O kolik se prodlouží tyč délky l a průřezu S působením vlastní tíhy, je-li na jednom konci upevněná? Hustota materiálu je ρ, modul pružnosti v tahu  je E. Uvažujte, že se jedná o pružnou deformaci - platí Hookův zákon.

[Návod: použijte Hookův zákon, vyjádřete prodloužení elementu tyče, pak zintegrujte.]

     Výsledek

     Příklad 6

Řešte příklad 5 za předpokladu, že ke konci tyče je zavěšeno závaží o hmotnosti m.

     Výsledek

     Příklad 7

Síla, která je potřeba k prodloužení kovového sloupku délky a na délku a + x, se rovná

kde k je konstanta. Vypočtěte práci vykonanou prodloužením sloupku délky a na délku b.

     Výsledek

    Příklad 8

Určete moment setrvačnosti homogenního rotačního válce o hmotnosti m a poloměru R vzhledem k podélné ose válce.

     Výsledek

     Příklad 9

Dokažte pomocí integrálního počtu, že těžiště rovnostranného trojúhelníka je ve vzdálenosti 1/3 výšky od základny.

     Příklad 10

Střední hodnota

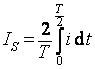
periodicky proměnného proudu i = I₀ sin ωt, kde

je hodnota stejnosměrného proudu, kterým se přenese stejný elektrický náboj. Určete I_S pro sinusový proud i = I₀ sin ωt.

     Výsledek

    Příklad 11

Tlak a objem plynu jsou vázány vztahem pV ^κ = C, kde κ = 1,4; C je konstanta.

a) Vypočtěte práci vykonanou stlačením 1024 m³ plynu tlakem 18 Pa na objem 243 m³.

b) Ukažte, že práce vykonaná stlačením plynu s tlakem p₁ z objemu V₁ na objem V₂ je

     Výsledek

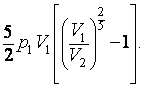
     Příklad 12

Kolik tepla je třeba na izotermickou expanzi 2 litrů  vodíku o tlaku 0,08 MPa na čtyřnásobný objem? Jaký bude výsledný tlak?

     Výsledek