Proč se zabývat křivkami?

S řadou křivek popisovaných v tomto textu se můžeme setkat v běžném životě a technické praxi. Na úvod si ukážeme jen několik aplikací, v dalším textu se pak na jednotlivé křivky v dalších částech textu zaměříme podrobněji včetně historie a matematického popisu.

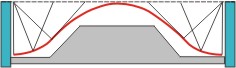Pokud jezdíte autobusem nebo tramvajemi - všimněte si: je-li nejnižší schůdek dveří zaprášen,  je vidět  křivka, jejíž stopy  je možno vidět v prachu při zavírání a otevírání dveří - pak mezi body A a A' vlevo uvedeného obrázku, je možno vidět část asteroidy.

 Archimédova spirála je křivka, kterou opisuje bod pohybující se stálou rychlostí po polopřímce, která se otáčí stálou rychlostí kolem počátku. Archimédovu spirálu vytváří např. moucha lezoucí po gramofonové desce ve směru jejího poloměru nebo po hodinové ručičce.

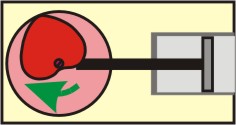
Pokud bychom vyrobili součástku tvaru, který odpovídá dvěma částem Archimédovy spirály, jak je znázorněno na obr. vlevo, a připevnili tuto součástku na otáčející se kruhový kotouč, dostaneme zařízení, které převádí rovnoměrný otáčivý pohyb na rovnoměrný posuvný pohyb pístu tam a zpět.

Kdyby moucha z gramofonové desky vzlétla, její křidélka nevykonávají jednoduché kmity (jak bychom si asi na první pohled mysleli), ale složitější pohyb ve tvaru "osmičky" - tzv. lemniskáty.

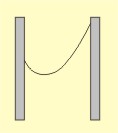Když zavěsíme např. řetěz (nebo jakékoliv dokonale ohebné nepružné vlákno) na dvou místech, která nejsou přímo nad sebou a jejichž vzdálenost je menší než délka řetězu, prohne se řetěz působením tíhového pole do tvaru křivky, kterou nazýváme řetězovka.

S další (pro vás zatím neobvyklou křivkou) je možno se setkat na atletické dráze. Závodní běžecká dráha má délku 400 m (měřeno ve vzdálenosti 30 cm od vnitřního okraje dráhy). Při běhu na 3000 m překážek je start v místě, kde přímka přechází do zatáčky. Je zřejmé, že pokud by každý závodník běžel neustále ve své dráze, byla by jeho trať delší než 3000 m. 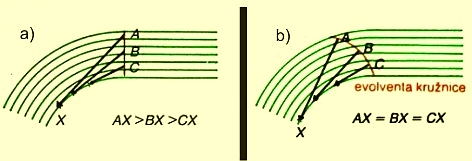Proto se každý závodník snaží běžet z místa startu přímočaře po tečně k okraji vnitřní dráhy. Podíváme-li se na obr. a), je zřejmé, že kdyby byla startovní čára kolmá na vyznačené dráhy, byli by závodníci z vnějších drah v nevýhodě. 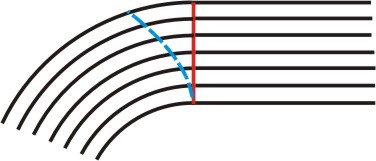Má-li být závod spravedlivý, musí mít startovní čára takový tvar, aby všichni závodníci proběhli stejně dlouhou trať - tomuto požadavku vyhovuje křivka nazývaná evolventa kružnice. (Když pořadatelé připravují trať na 3000 m překážek, odměří provaz dlouhý 23 m, provaz pak navinou na obrubník vnitřní dráhy, jeden konec uchytí v bodě X - obr. vpravo. Potom druhým koncem vyznačí při odvíjení provazu od obrubníku startovní čáru v požadovaném tvaru evolventy kružnice).

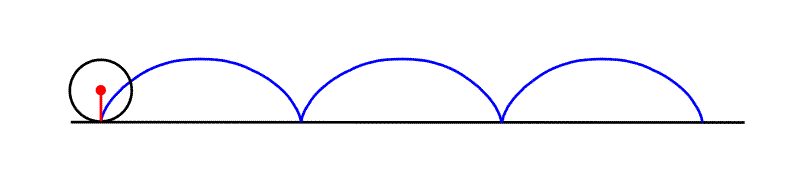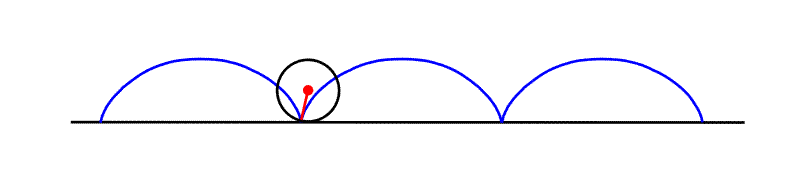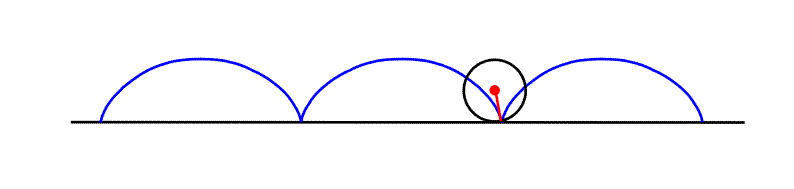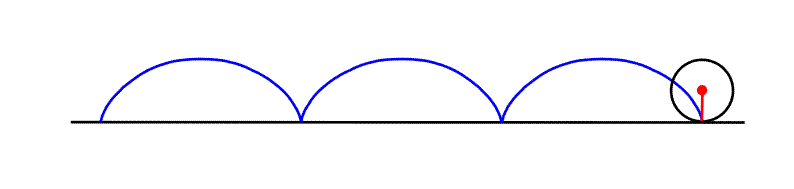
Pokud byste se dále zamysleli nad tím, kde jste se už s setkali s křivkami ve svém životě, zcela jistě jste byste přišli i na další křivku, která vzniká např. při valivém pohybu kola automobilu na rovné vozovce - tzv. cykloidu. Kolo by se ale také mohlo odvalovat po nějakém válci uvnitř nebo i vně a to má za následek vznik dalších křivek - epicykloidy a hypocykloidy.

Možná byste přišli i na některé další křivky - je ale nutné si uvědomit, že objevení a zkoumání těchto křivek je prováděno už po několik staletí řadou velmi význačných matematiků a fyziků.

Řadu křivek je možno také si vykreslit pro předem zvolené parametry pomocí modelování. Text je také doplněn řadou animací jednotlivých křivek, kde se to jeví jako vhodné.

Cílem tohoto textu je provést seznámení alespoň s těmi nejvýznačnějšími křivkami, protože v dnešní době je těch křivek již velmi mnoho. Vzhledem k omezenému rozsahu textu jsou zde uvedeny  hypertextové odkazy i na další křivky, které byly  až do současné doby objeveny a zkoumány.

Nyní se již můžeme začít věnovat jednotlivým křivkám podrobněji.