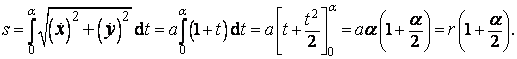[Zpět na stránku Matematika křivek]

Archimédova spirála

Historie a užití

Helix

Příklad

Matematický popis spirály

Rovnice má v polárních souřadnicích tvar

kde a je dané kladné číslo.

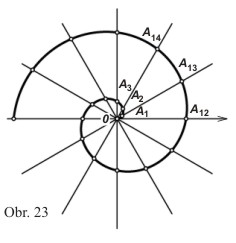
Z rovnice spirály nyní nakreslíme tvar spirály.

Úhel 2π  s vrcholem O (počátek soustavy souřadnic) rozdělíme na několik stejných částí, v našem případě zvolíme 12 částí. Z bodu O pak povedeme 12 dělicích polopřímek (obr. 23). Tyto polopřímky budou svírat s polární osou po řadě úhly

Z rovnice křivky nalezneme příslušné hodnoty průvodičů

Nyní už jen vezmeme libovolnou úsečku a budeme předpokládat, že její délka je 2πa.

     K sestrojení bodů spirály, které leží na zvolených polopřímkách, zbývá už jen nanést na tyto polopřímky od pólu délky rovné

Tímto způsobem dostaneme body A₁, A₂, A₃ atd.

     Abychom sestrojili body, které odpovídají hodnotám φ > 2π, provedeme následující úvahu. Nechť

příslušná hodnota průvodiče pak bude

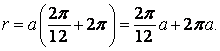
Tato hodnota se liší od hodnoty r příslušející prvnímu bodu, který leží na vyšetřované polopřímce o 2πa (tj. o délku námi zvolené úsečky). Prodloužíme-li nyní první polopřímku a naneseme na ni od bodu

už dříve sestrojeného, úsečku délky 2πa, dostaneme zase bod křivky, na obr. 23 to bude bod A₁₃.

     Stejně můžeme sestrojit i body na ostatních polopřímkách, protože hodnoty úhlu φ se budou pro nové lišit od hodnot φ pro body dříve sestrojené pokaždé o 2π.

Parametrické vyjádření

Archimédovu spirálu je také možné modelovat na počítači. K tomu je třeba od souřadnic polárních přejít k souřadnicím parametrickým. Vhodné je v tomto případě např. zvolit

Délka Archimédovy spirály

Délka Archimédovy spirály je konečná a určíme ji užitím vztahu (14) pro výpočet délky křivky v parametrickém vyjádření.

Určíme délku spirály od počátku do nějakého bodu A na spirále, jehož poloha je dána souřadnicemi r, α. Nejprve určíme

Dále je

Po dosazení do vztahu (14) pro délku křivky je