Historie
Tyto křivky studovali Dührer (1525), Desargues (1640), Huygens (1679), Leibniz, Newton (1626), l'Hospital (1690), Jacob Bernoulli (1690), la Hire (1694), Johann Bernoulli (1695), Daniel Bernoulli (1725), Euler (1745, 1781).
Např. Epitrochoidu objevil Dührer ve své práci Instruction in measurement with compasses and straight edge (1525).
Konstrukce epicykloidy a hypocykloidy
Speciální případy a užití - rhodonea (modelování)
Parametrické rovnice epicykloidy a hypocykloidy
a) Prostá epicykloida a hypocykloida
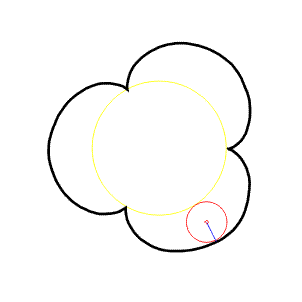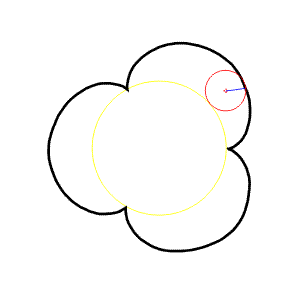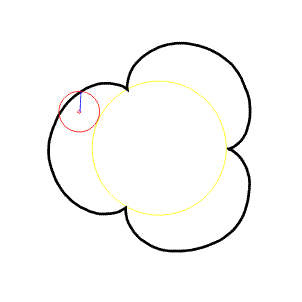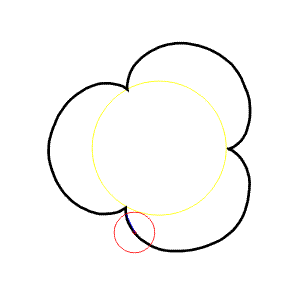
Epicykloida
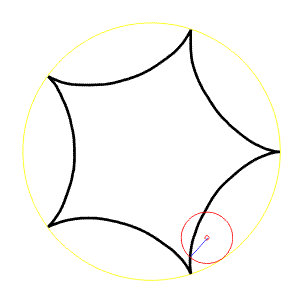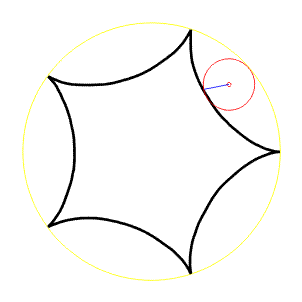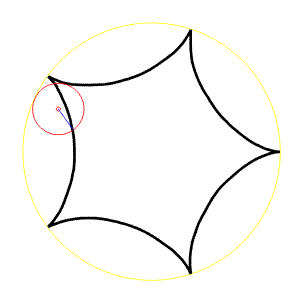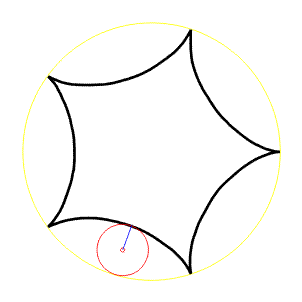
Odvalování vně kružnice, označíme a - poloměr pevné kružnice (žlutá), r- poloměr pohyblivé kružnice (červená). Potom
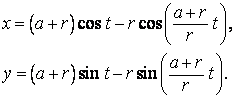
Je-li poměr a/r = m celé číslo, pak prostá epicykloida je uzavřena křivkou s m větvemi, které vzniknou při jednom oběhu hybné kružnice kolem nehybné kružnice.
Je-li poměr a/r = p/q = m racionálním číslem v základním tvaru p/q, pak prostá epicykloida je uzavřenou křivkou s p větvemi, které vzniknou při q obězích hybné kružnice kolem nehybné kružnice.
Je-li poměr a/r = m iracionálním číslem, pak prostá epicykloida není uzavřenou křivkou a obsahuje nekonečně mnoho větví.
Délka větve
![]()
Délka prosté epicykloidy pro m Î Z: l = 8(a + r).
Obsah plochy ohraničené jednou větví prosté epicykloidy a příslušným obloukem nehybné kružnice
![]()
Hypocykloida
Odvalování uvnitř kružnice, označíme a - poloměr pevné kružnice (žlutá), r- poloměr pohyblivé kružnice (červená). Potom
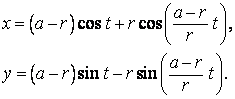
Je-li poměr a/r = m celé číslo, pak prostá hypocykloida je uzavřena křivkou s m větvemi, které vzniknou při jednom oběhu hybné kružnice kolem nehybné kružnice.
Je-li poměr a/r = p/q = m racionálním číslem v základním tvaru p/q, pak prostá hypocykloida je uzavřenou křivkou s p větvemi, které vzniknou při q obězích hybné kružnice kolem nehybné kružnice.
Je-li poměr a/r = m iracionálním číslem, pak prostá hypocykloida není uzavřenou křivkou a obsahuje nekonečně mnoho větví.
Délka větve
![]()
Délka prosté hypocykloidy pro m Î Z: l = 8(a - r).
Obsah plochy ohraničené jednou větví prosté epicykloidy a příslušným obloukem nehybné kružnice
![]()
b) Prodloužená a zkrácená epicykloida a hypocykloida
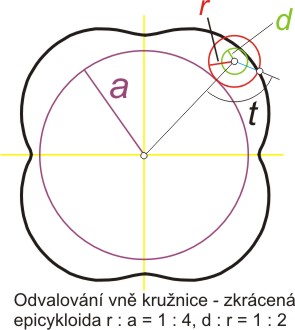
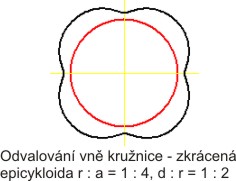
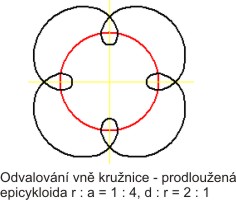
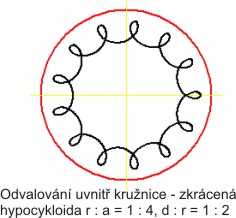
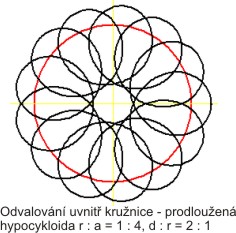
Epicykloida prodloužená a zkrácená
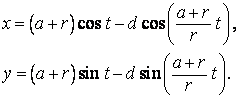
Prodloužená - d/r > 1, zkrácená - d/r < 1.
Hypocykloida prodloužená a zkrácená
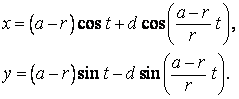
Prodloužená - d/r > 1, zkrácená - d/r < 1.