[Zpět na stránku Matematika křivek]

Epicykloidy a hypocykloidy - speciální případy, užití

a) Prostá epicykloida

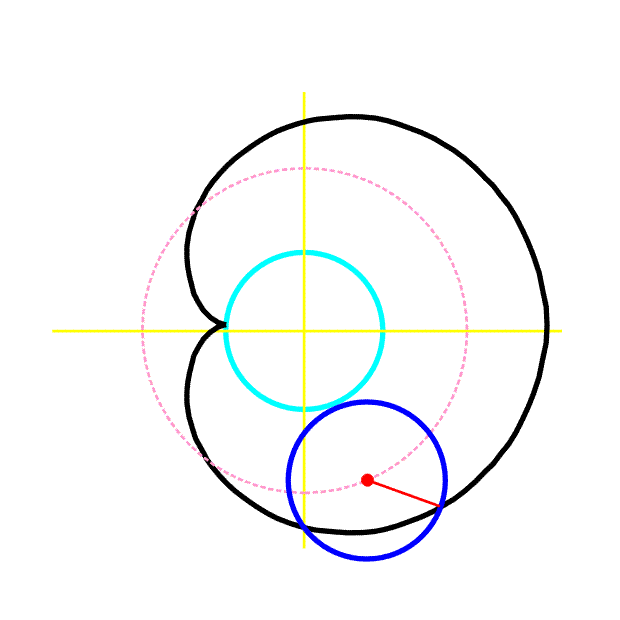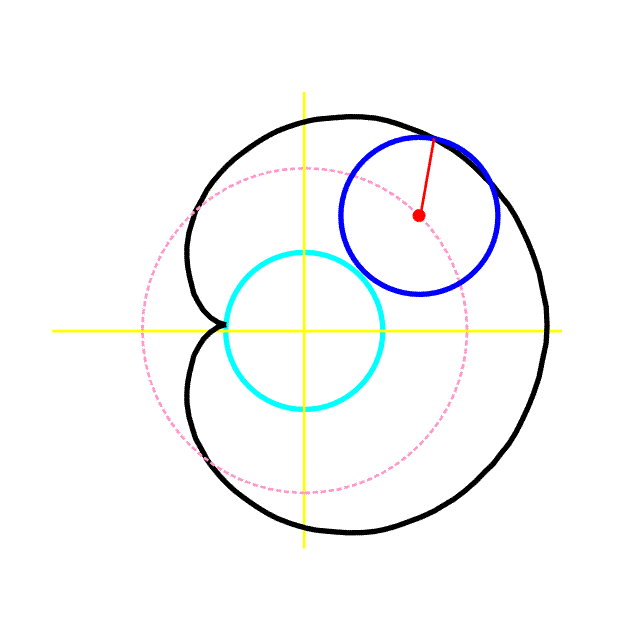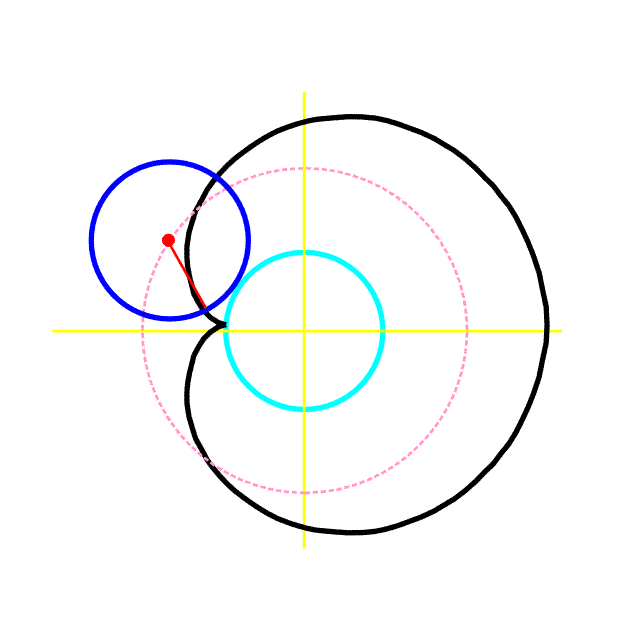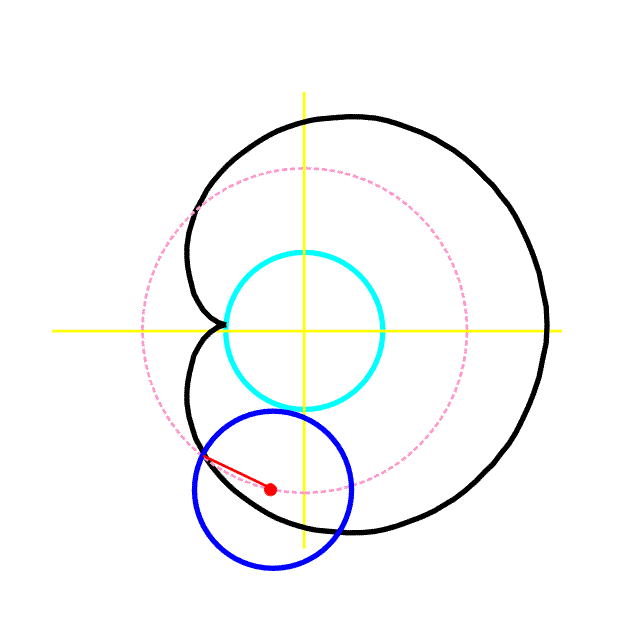
Pro a = r  má prostá epicykloida (kardioida) parametrické rovnice

O kardioidě je více zde, délka kardioidy je vypočtena zde.

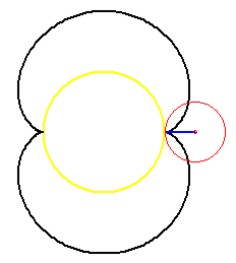
Pro r = a/2 má prostá epicykloida (nefroida) parametrické rovnice

Historická poznámka

Jméno nephroida (znamená "podoba ledviny") použil pro dva oblouky epicykloidy Proctor v roce 1878. Nefroida má délku 24a a plochu 24π²a².

Huygens v roce 1678 pozoroval, že nefroida je kataustika kružnice, když zdroj světla je v nekonečnu. Toto publikoval v Traité de la Lumièrein v roce 1690. Vysvětlení proč ale nepodal a podala ho teprve vlnová teorie světla. Teoretický důkaz předložil Airy v roce 1838.

b) Prostá hypocykloida

Pro r = a/2 má prostá hypocykloida parametrické rovnice

Je to tedy úsečka délky 2a v ose x.

Tohoto poznatku se využívá k přeměně otáčivého pohybu v pohyb sem a tam, což má technické použití při řezání ozubení.

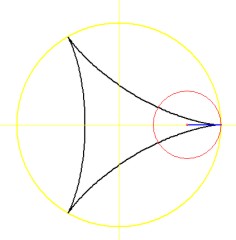
Pro r = a/3 má prostá hypocykloida (Steinerova) parametrické rovnice

Pro r = a/4 má prostá hypocykloida (asteroida) parametrické rovnice

Délka asteroidy je vypočtena zde.

c) Prodloužená epicykloida

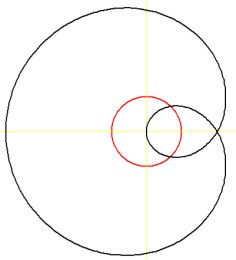
Je-li r = a, d > r, dostáváme prodlouženou epicykloidu (Pascalovu závitnici) v parametrických rovnicích

d) Prodloužená nebo zkrácená hypocykloida

Zkrácená a prodloužená hypocykloida přechází pro m = 2, tj. pro d ≠ r = a/2 v elipsu s rovnicemi (t Î R)

Tohoto poznatku se využívá k přeměně otáčivého pohybu v eliptický pohyb.