Šroubovice (helix)
Fotogalerie stažená z Internetu
Vztah šroubovice a cykloidy (z deskriptivní geometrie)
Matematický popis šroubovice
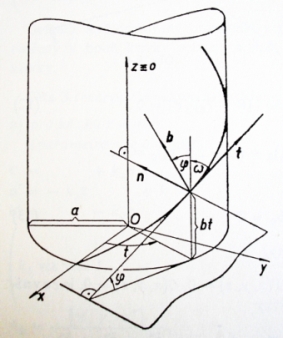Šroubovice
je křivka daná parametrickými rovnicemi
Tato křivka leží na rotační válcové ploše
(což lze obdržet vyloučením parametru z prvních dvou parametrických rovnic).
Derivací vztahů (18) dostaneme
Rozvineme-li válcovou plochu, na níž šroubovice leží, do roviny, rozvine se zároveň každý závit šroubovice do úsečky svírající s úsečkou vzniklou rozvinutím kružnice na válci úhel φ.
Nyní bychom chtěli zjistit délku oblouku jednoho závitu šroubovice. Vztah (14) pro výpočet délky oblouku v rovině je možno zobecnit na tvar, který lze použít v prostoru
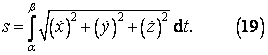
Připomeňme si, že výraz pod odmocninou vyjadřuje velikost okamžité rychlosti.
Nyní určíme
Po dosazení do (19) dostaneme
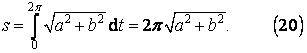
Poznámka
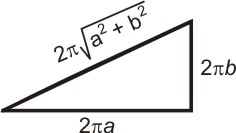
Vztah (20) je vidět téměř okamžitě z rozvinutí na obrázku vlevo. Označíme
Nyní se pokusíme místo výpočtu délky celého jednoho oblouku šroubovice spočítat jen část délky oblouku. Vztah (20) lze pak přepsat do tvaru
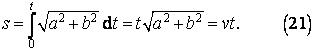
Vzhledem k tomu, že velikost rychlosti pohybu hmotného bodu po šroubovici je konstantní, vyjadřuje vztah (21) závislost dráhy na čase pro rovnoměrný pohyb.