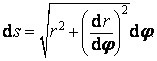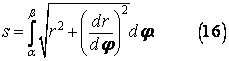 Délku
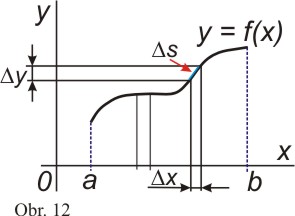
křivky určíme tak, že si celou křivku rozdělíme na n částí, které
můžeme přibližně považovat za přímky. Potom pro délku takového dílku platí
Délku
křivky určíme tak, že si celou křivku rozdělíme na n částí, které
můžeme přibližně považovat za přímky. Potom pro délku takového dílku platí
![]()
Zvolíme-li dílky velmi malé, můžeme Δ - přírůstky nahradit diferenciálem funkce, tj.
![]()
Po úpravě dostaneme tzv. diferenciál oblouku křivky
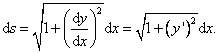
Celou délku křivky pak dostaneme integrací
![]()
Parametrické vyjádření křivky
Je-li křivka dána parametricky, tj.
![]()
Potom můžeme psát
![]()
Po dosazení do (12) dostaneme
![]()
po odmocnění je diferenciál oblouku křivky dán vztahem
![]()
Celková délka křivky je pak dána vztahem
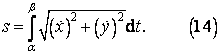
Poznámka
Jestliže budeme parametr t považovat za čas, potom výraz s odmocninou vyjadřuje velikost okamžité rychlosti pohybu. Potom lze psát
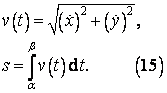
Polární souřadnice
Je-li rovnice křivky zadána pomocí polárních souřadnic r a φ, pak můžeme psát
![]()
Potom
![]()
Po dosazení do (12) dostaneme
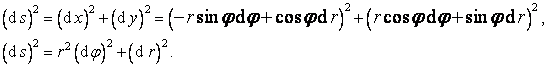
Po úpravě a odmocnění