Šroubovice - příklad
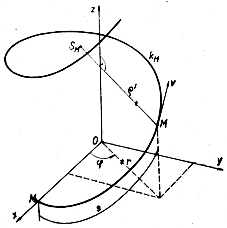
Pohyb
bodu M po válcové šroubovici se stálým stoupáním je dán rovnicí
kde
Vypočtěte časový průběh dráhy, rychlosti a zrychlení, dále průběh tečného a normálového zrychlení a poloměr křivosti.
Je dáno: r = 10 m, ω = 1 s-1, c = 2 m·s-1.
Řešení
Pro rychlost můžeme psát
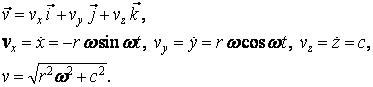
Zrychlení pohybu určíme opět derivací
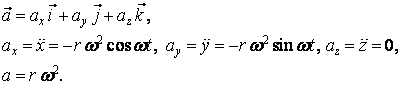
Rychlost i zrychlení jsou co do velikosti stálé.
Pro normálovou a tečnou složku zrychlení platí:
Poloměr křivosti je dán vztahem
kde α je úhel stoupání šroubovice.
Závislost s = s(t) určíme užitím vztahu (14), který přepíšeme na tvar v prostoru
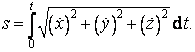
Potom
což lze ale také napsat přímo (protože jde o rovnoměrný pohyb) jako
Pro dané hodnoty: s = 10,2 t [m], v = 10,2 ms-1, a = 10 ms-2, ρ = 10,4 m.
Ke stejným výsledkům lze dospět také užitím válcových souřadnic.