
Se spirálami je možno se setkat prakticky všude. Jedním z prvních, kdo před 2300 lety popsal tuto křivku, byl Archimédes. Tzv. Archimédova spirála se vyskytuje např. při pohybu bodu, který se pohybuje po polopřímce od jejího počátečního bodu v pólu O konstantní rychlostí, zatímco polopřímka sama se otáčí kolem pólu při konstantní úhlové rychlosti (může se jednat např. o pohyb mouchy po hodinové ručičce). Archimédova spirála se také vyskytuje v různých mechanismech ve strojnictví jako tzv. Archimédův šroub (technicky se této křivce říká závitnice). Na jejím principu pracují vrtáky, šroubky a různé šrouby. Tvaru spirály se říká helix a právě takové spirály se asi nejčastěji v technické praxi. také popínavé rostliny šplhají ke Slunci se závity typu helix, tak, jak tuto spirálu popsal Archimédes.

 Vačkový
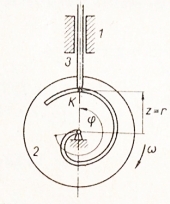
mechanismus na obr. je tvořen kotoučem, v němž je vyfrézována drážka tvaru
Archimédovy spirály, a centrickým zvedákem 3, který je opatřen
kladkou K, vedenou v drážce. Dokažte, že rovnoměrnému otáčení vačky
odpovídá rovnoměrný posuv zvedáku (konstantní převod).
Vačkový
mechanismus na obr. je tvořen kotoučem, v němž je vyfrézována drážka tvaru
Archimédovy spirály, a centrickým zvedákem 3, který je opatřen
kladkou K, vedenou v drážce. Dokažte, že rovnoměrnému otáčení vačky
odpovídá rovnoměrný posuv zvedáku (konstantní převod).
Dále odvoďte rovnici spirály, má-li dávat zdvih h = 16 mm na jedno otočení vačky.
Řešení:
Rovnice Archimédovy spirály má obecně tvar
![]()
Okamžitý zdvih zvedáku
![]()
a jeho rychlost, jestliže je otáčení vačky rovnoměrné
![]()
je tedy také stálá.
Pro zdvih h = 16 mm má rovnice spirály tvar
![]()