Ukažme si použití limity funkce na konkrétním příkladu ze studijního textu Pohyb těles s vlivem odporových sil - formát PS, popř. Pohyb těles s vlivem odporových sil - formát PDF - str. 8.
Kulička o poloměru
r je ponořena do vody, přičemž hustota r kuličky je jen o málo větší než hustota r v vody. Kuličku z její výchozí polohy pustíme nulovou počáteční rychlostí. Vypočtěte: závislost rychlosti kuličky na čase, mezní rychlost kuličky.S ohledem na zadanou relaci hustot předpokládáme laminární obtékání a pro odporovou sílu použijeme Stokesův vztah
![]()
Na kuličku bude působit ještě tíhová a
vztlaková síla. Osu y zvolíme kladně ve směru tíhového zrychlení g s počátkem ve výchozí poloze kuličky. Počáteční podmínky úlohy jsou tedy: y (0) = 0, v (0) = 0.Pohybová rovnice pak je
![]()
Vyjádříme-li hmotnosti pomocí hustot a dosadíme
za síly F vz , F o , dostaneme
![]()
Tuto pohybovou rovnici můžeme přepsat formálně do tvaru
![]()
kde
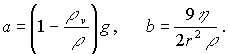
Pokud bychom výše popsanou rovnici vyřešili - převedením na tzv. diferenciály a následně vzniklou diferenciální rovnici vyřešili (viz výše uvedený studijní text str. 9), dostaneme
![]()
Mezní rychlost dostaneme z výše uvedeného vztahu pro t ® ¥ .
Určíme limitu výrazu pro rychlost
![]()
Nejprve určíme
![]()
S použitím této vypočtené limity dostaneme
![]()
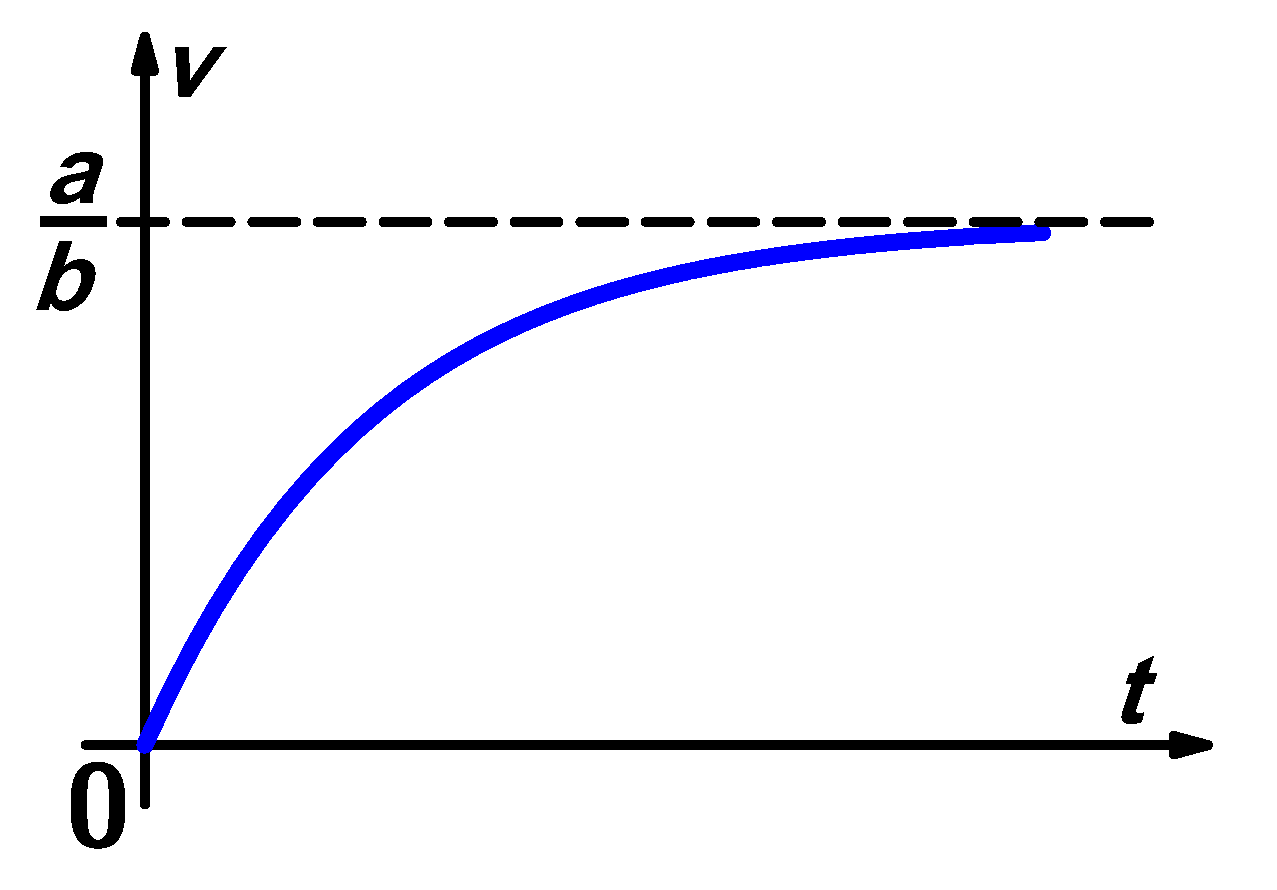
Graf závislosti rychlosti na čase
v = v(t) pro t ® ¥ je uveden níže.