Vyšetřete průběh funkce
![]()
v okolí bodu x = 1 .
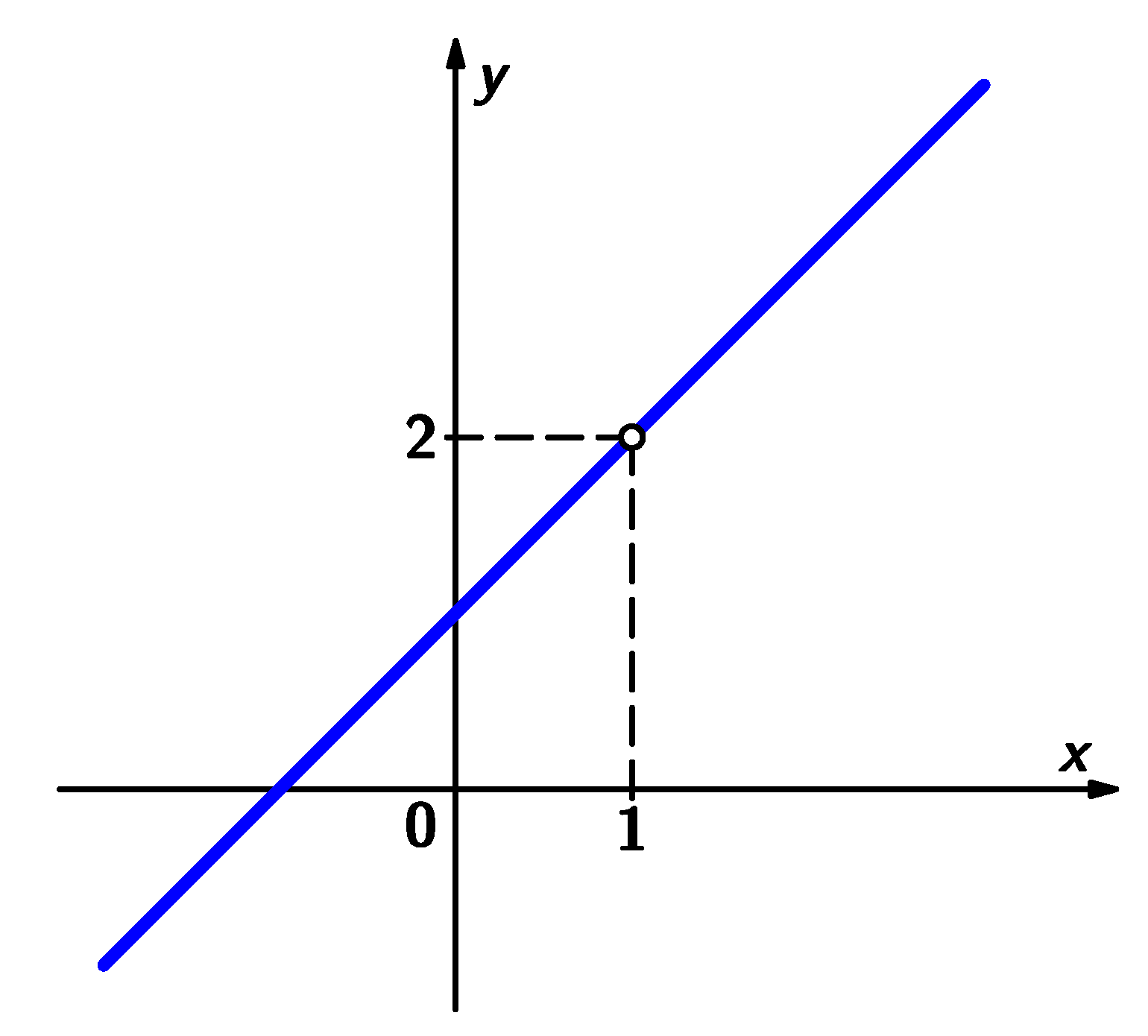
Zadaná funkce má stejné hodnoty jako funkce
![]()
pro všechna x ¹ 1. Funkce
![]()
není v bodě
x = 1 definována na rozdíl od funkce
![]()
která má v tomto bodě hodnotu
y 2 = 2. Ke stejné hodnotě se však hodnoty funkce y 1 v tomto bodě blíží. Říkáme, že funkce y 1 má v bodě x = 1 limitu rovnou 2 a zapisujeme
![]()
Zvolíme-li jakékoliv malé kladné číslo e
, dovedeme nalézt takové okolí bodu x = 1, že se v něm hodnoty funkce y 1 budou lišit od 2 o méně než e . Matematicky to lze vyjádřit takto:
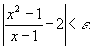
Tento závěr je možno zformulovat obecně:
Funkce
![]()
má v bodě
x 0 limitu rovnou a , jestliže existuje kladné číslo d tak, že nerovnost
![]()
platí pro všechna x , pro která
![]()
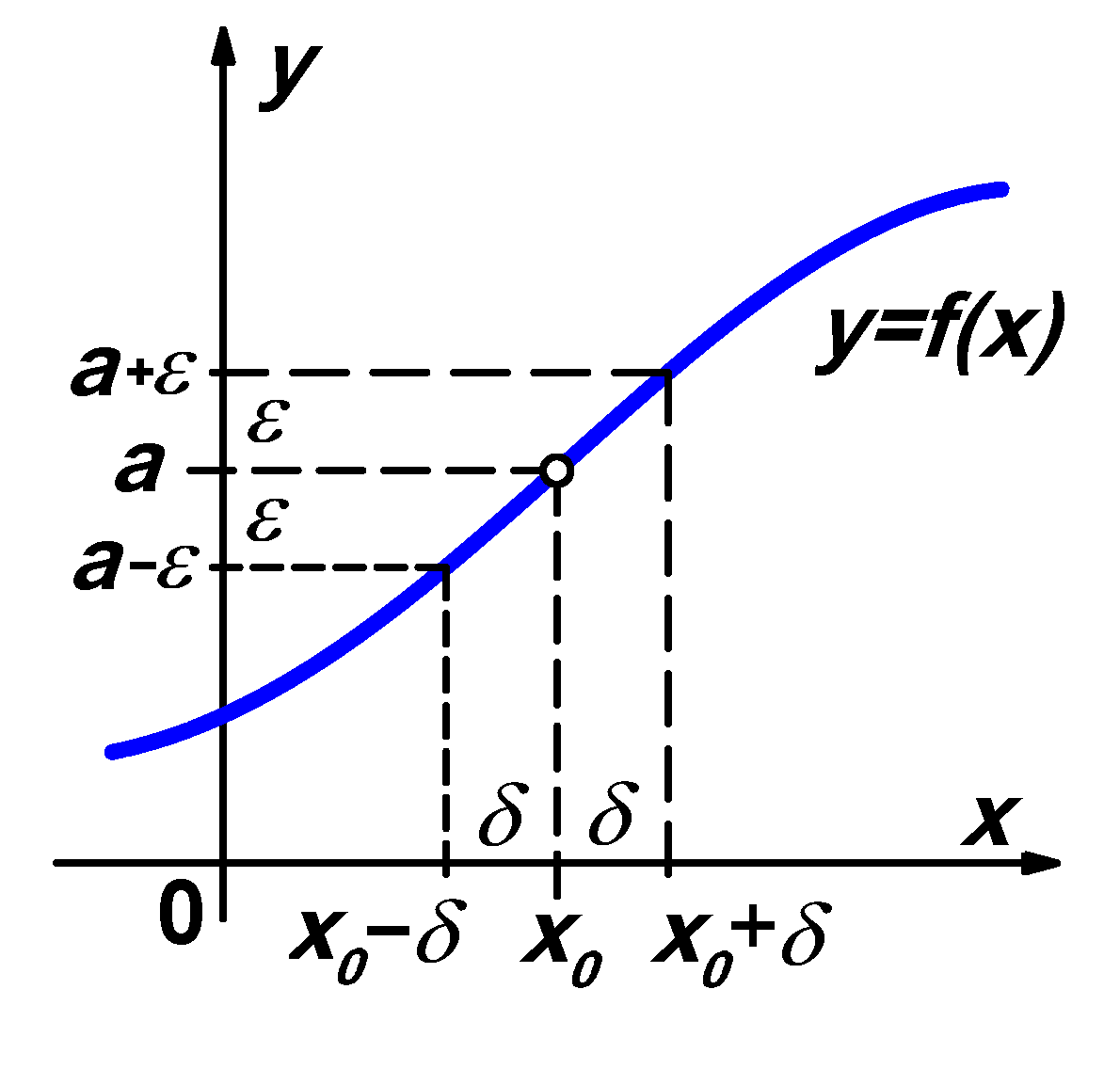
Zapisujeme
![]()
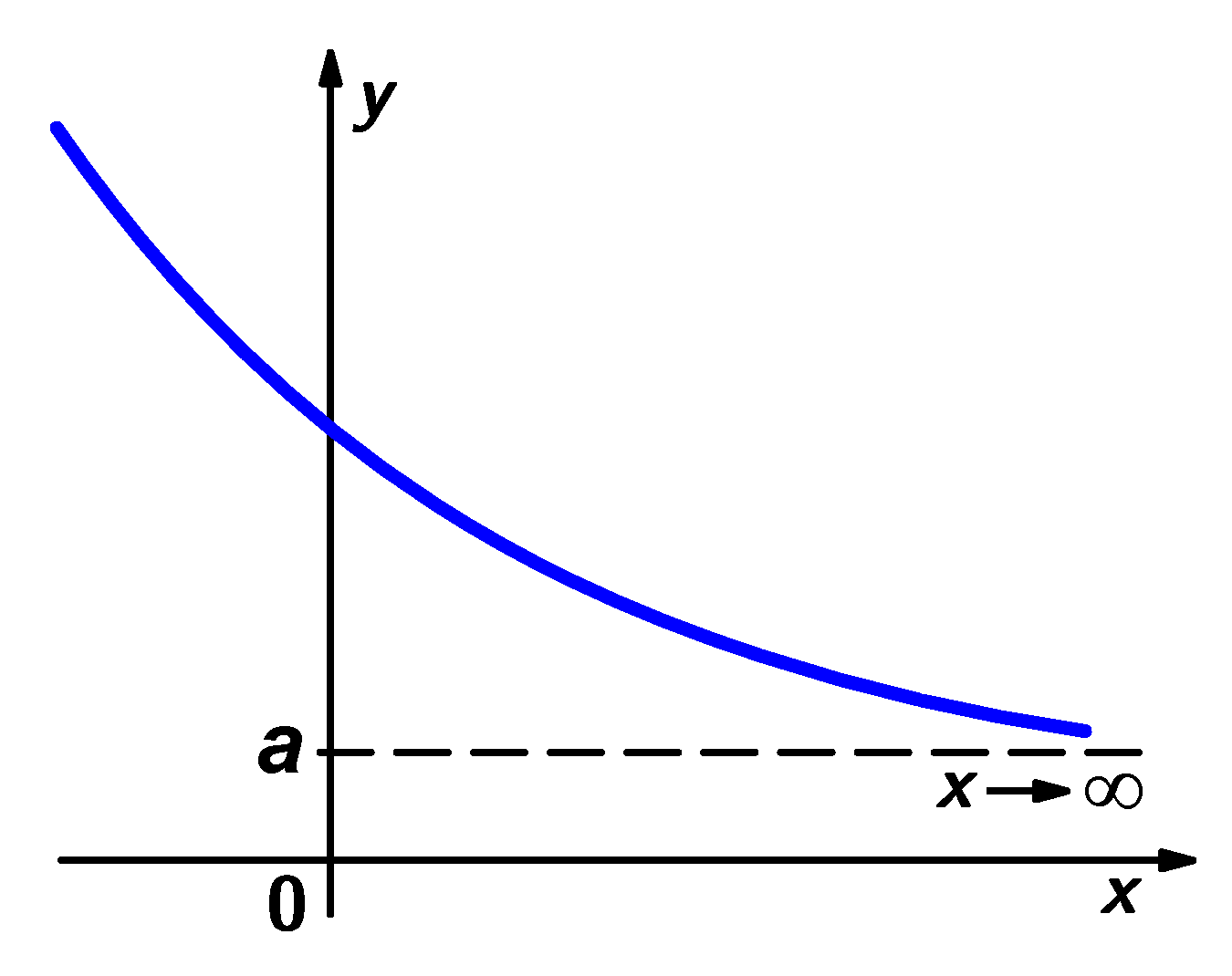
Je-li a , x 0 konečné, má funkce
![]()
ve vlatním bodě vlastní limitu.
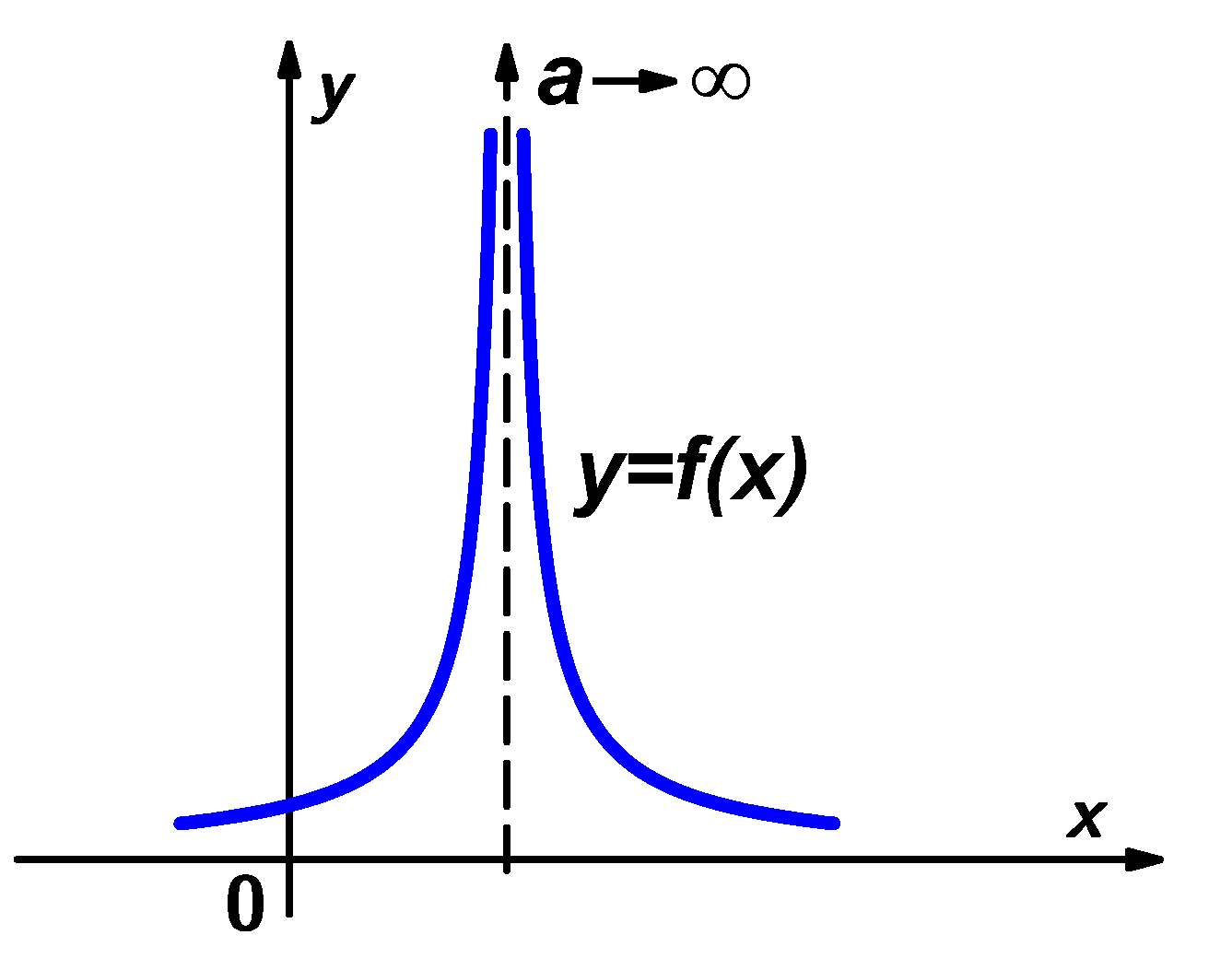
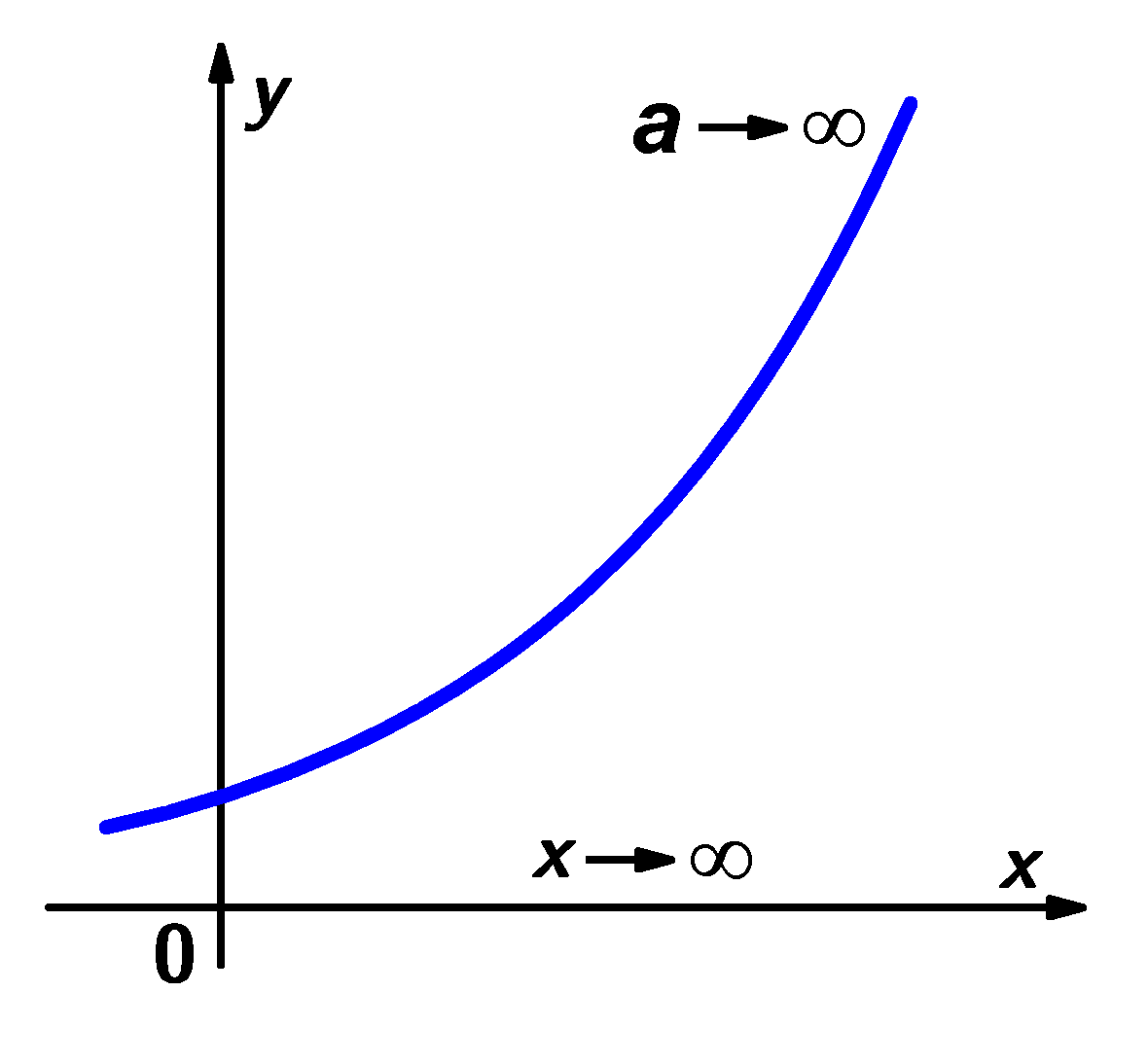
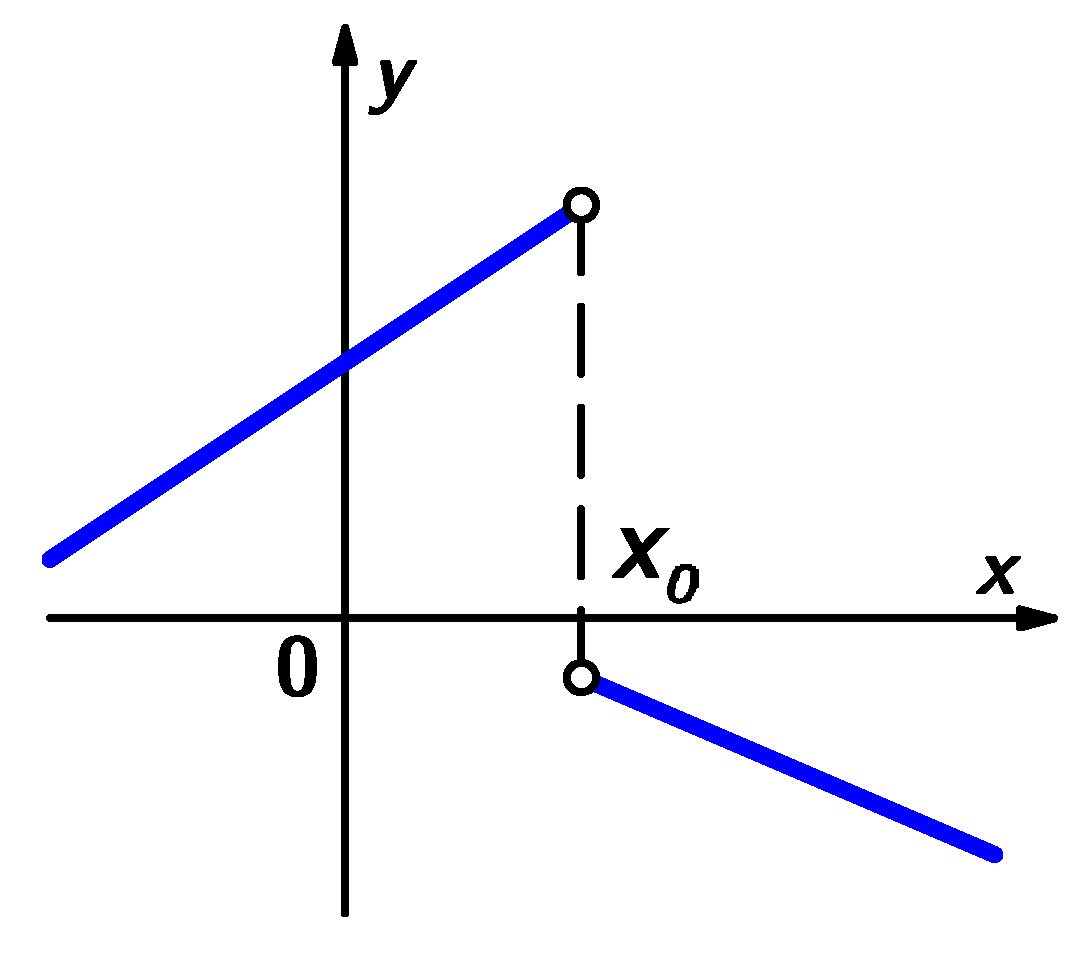
![]()
Např. funkce
![]()
má pro x ® 0 nevlastní limitu zleva - ¥ , zprava + ¥ .
Zapisujeme:
![]()
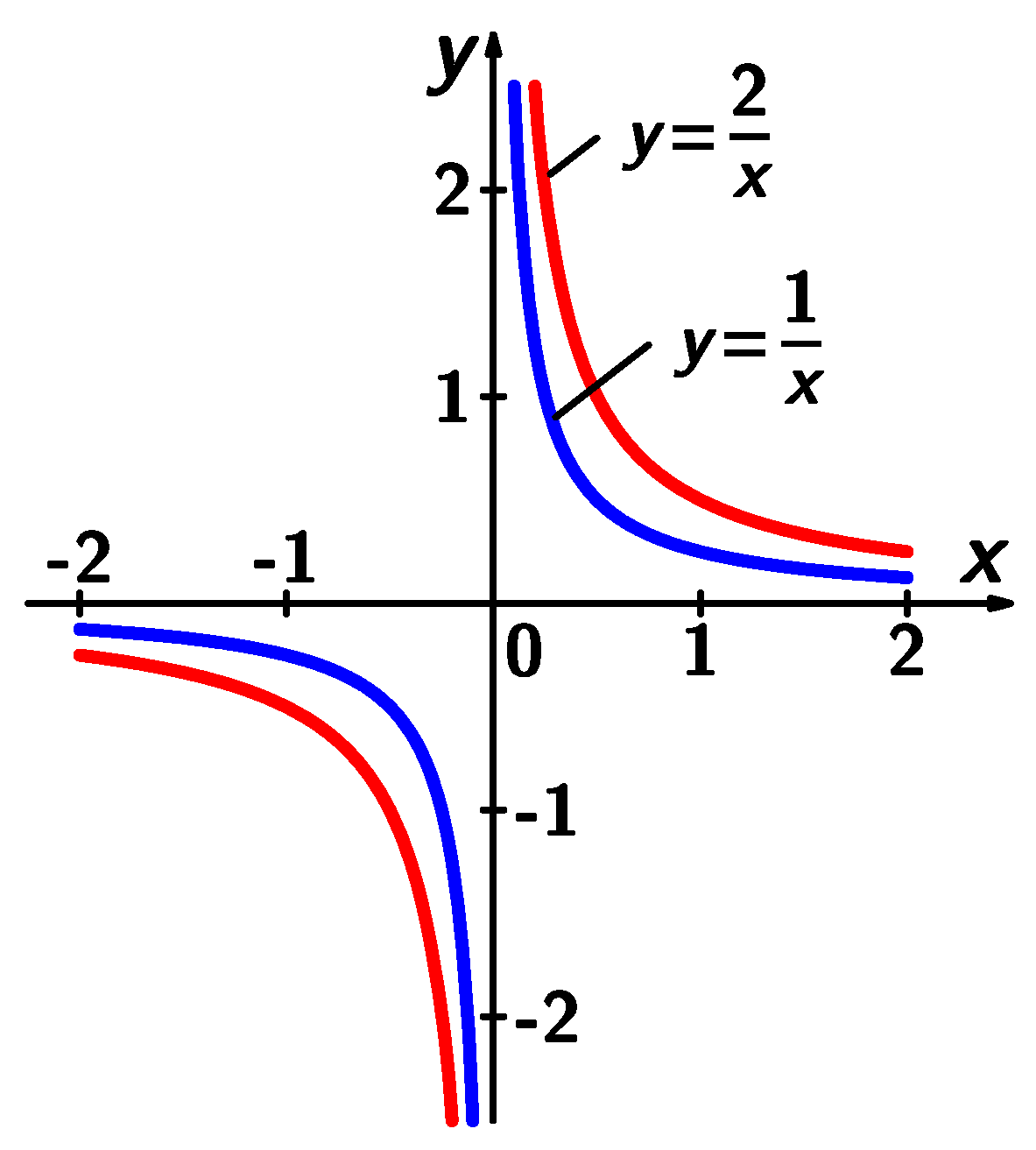
3. Má-li funkce f(x) v bodě x 0 oboustrannou limitu a , pak platí:
![]()
Pro výpočet limit funkcí si dále uvedeme velmi důležité věty , které jsou obdobné jako věty o limitách posloupností.
Nechť funkce
f(x) , g(x) mají v bodě x 0 vlastní limity a , b , tj.
![]()
Potom platí
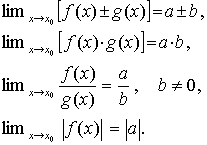
Tato pravidla platí také pro více funkcí.
Některé důležité limity často užívané při výpočtech:
![]()
Pro výpočty limit dále platí:
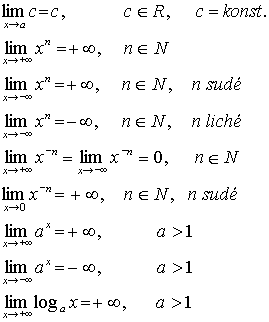
![]()
ani
![]()
neexistuje pro
![]()