Mechanika
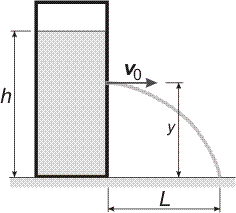
| Příklad 1 Voda v nádobě má hladinu ve výšce h = 30 cm. Jak vysoko nad dnem je třeba vyvrtat ve stěně nádoby otvor, aby voda stříkala co nejdále na vodorovnou rovinu, na které je nádoba položená?
|
 |
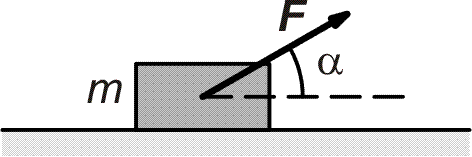
| Příklad 2 Těleso o hmotnosti m je taženo po vodorovné podložce rovnoměrně silou F, která svírá s podložkou úhel a. Součinitel smykového tření mezi tělesem a podložkou je f. Napište podmínku pro úhel a, která musí být splněna, aby síla F měla nejmenší velikost. (Při řešení úlohy uvažujte, že silové působení mezi tělesem a podložkou je rovnoměrné v celé styčné ploše.) Dále určete také obecně velikost této minimální síly. |
 |
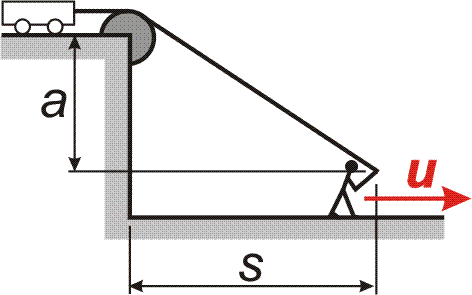
| Příklad 3 Po zemi běží dělník a táhne za provaz vozík, který je na zvýšeném náspu na kolejích. Vypočtěte rychlost vozíku a jeho zrychlení, běží-li dělník stálou rychlostí u a je-li konec provazu (ruka v očku) vzdálen od kolejí a m (viz obrázek vpravo). Za proměnnou volte dráhu dělníka.
|
 |
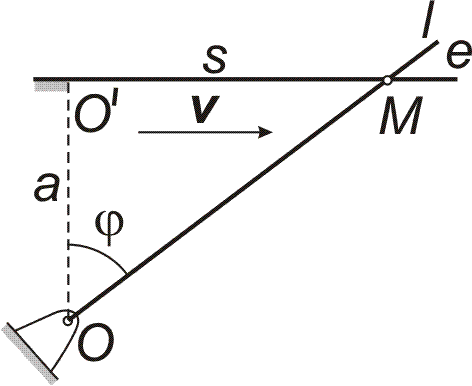
| Příklad 4 Tenká ocelová tyč se otáčí rovnoměrně s úhlovou rychlostí ω kolem vodorovné osy, která prochází jedním koncem tyče. Tyč prochází současně kroužkem, který se může posunovat po vodorovném drátu, jehož vzdálenost od osy otáčení je a (viz obrázek vpravo). Na počátku otáčení byla tyč ve svislé poloze, takže kroužek byl nad osou v bodě O´. Vypočtěte rychlost kroužku po drátě v závislosti na vzdálenosti s kroužku od bodu O´.
|
 |
Příklad 5
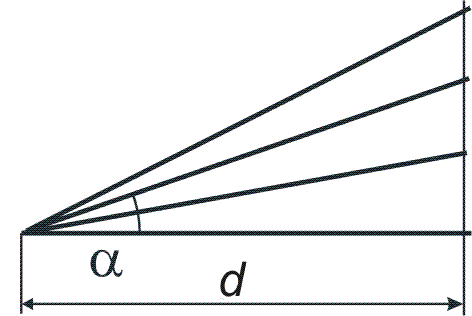
| Svazek částí nakloněných rovin má stejný průmět d
= 0,5 m do vodorovné roviny. Po rovinách necháme smýkat nějaké těleso.
Součinitel smykového tření mezi tělesem a nakloněnou rovinou je f
= 0,4. Pohyb se děje ve všech případech z klidu, vždy po celé délce
nakloněné roviny, a to pouze tíhovými účinky (g = 9,81 ms-2).
a) Jak dlouho se bude těleso pohybovat po jedné z nakloněných rovin při úhlu a = 450? b) Při jakém úhlu amin bude doba smýkání nejmenší a jak dlouho bude smýkání v tomto případě trvat? |
 |
Příklad 6
Dvě částice o hmotnostech m1 a m2 (m1 > m2) se pohybují po přímce rychlostmi o velikostech v1 a v2 (v1 > v2) stejné orientace tak, že dojde k jejich pružnému rázu (srážce). Ukažte, že nárůst kinetické energie částice o hmotnosti m1 bude maximální, jestliže se před srážkou pohybovala rychlostí
![]()
Při řešení předpokládejte, že ráz je dokonale pružný.
Příklad 7
Dvě částice o hmotnostech m1 a m2 (m1 > m2) se pohybují po přímce rychlostmi o velikostech v1 a v2 (v1 > v2) stejné orientace tak, že dojde k jejich nepružnému rázu (srážce). Ukažte, že nárůst kinetické energie částice o hmotnosti m1 bude maximální, jestliže se před srážkou pohybovala rychlostí
![]()
Při řešení předpokládejte, že ráz je dokonale nepružný.
Geometrická optika
|
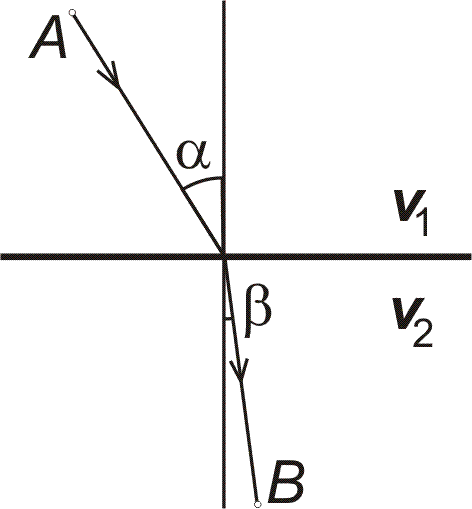
Příklad 8 (Fermatův princip nejmenšího času) Dvě různá optická prostředí jsou oddělená rovinným rozhraním. Určete, kterým směrem má postupovat světelný paprsek, aby z daného bodu v prvním prostředí dospěl do bodu B v druhém prostředí v co nejkratším čase (uvažujte, že světelný paprsek se v prvním prostředí pohybuje rychlostí o velikosti v1, ve druhém prostředí rychlostí o velikosti v2).
|
 |
Poznámka:
V předchozí úloze byl odvozen zákon lomu ve tvaru:
![]()
V optice se tento zákon ale častěji vyskytuje ve tvaru s indexem lomu n, který je definován jako podíl
![]()
kde c je rychlost světla ve vakuu, v je rychlost světla v daném prostředí. Zákon lomu je pak možno přepsat ve tvaru
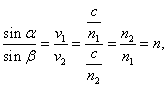
kde n je tzv. relativní index lomu.
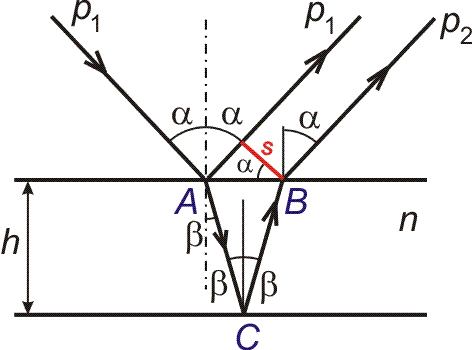
| Příklad 9 Na planparalelní skleněnou vrstvu (index lomu n) dopadá světelný paprsek pod úhlem a, částečně se odráží jako paprsek p1, částečně vniká do vrstvy a po odrazu na druhé straně vystupuje rovnoběžně s p1 jako paprsek p2. Při jakém úhlu a je vzdálenost s paprsků p1 a p2 největší?
|
 |
Příklad 10
Odvoďte zákon odrazu světla pomocí Fermatova principu nejmenšího času.
Fotometrie
Při řešení následujících úloh budeme využívat základní poznatky z fotometrie, před řešením úloh by bylo vhodné se na tuto část podívat do učebnice fyziky, ale není to nutné - níže je vysvětlen vztah používaný při řešení úloh.
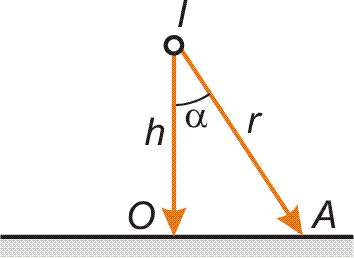
| Uvažujme zdroj o svítivosti I. Budeme se zabývat
výpočtem osvětlení E v závislosti na vzdálenosti od zdroje a
úhlu dopadu.
Pro osvětlení E0 v bodě O (kolmý dopad) platí vztah:
Pro osvětlení EA v bodě A platí jiný vztah (ale výše uvedený vztah se dá pojmout jako jeho speciální případ):
|
 |
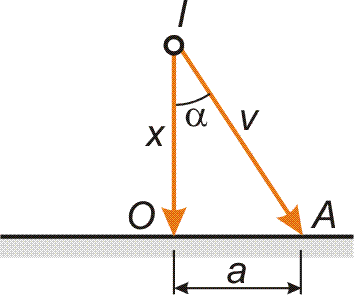
| Příklad 11 Kruhový objezd na křižovatce, jehož střední kružnice má od středu celé kruhové plochy vzdálenost a = 10 m, má být osvětlen stožárovou lampou stojící právě ve středu kruhu. Jak vysoký musí být stožár, aby vozovka (uvažováno ke střední kružnici), byla co nejvíce osvětlena?
|
 |
|
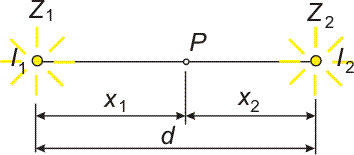
Příklad 12 Ve vzdálenosti 30 m od sebe jsou dva zdroje světla. Jejich svítivosti jsou v poměru 27 : 8. Najděte na spojnici nejméně osvětlený bod. |
 |
Elektrické obvody
Příklad 13
Máme k dispozici n = 36 solárních článků o
elektromotorickém napětí Ue = 0,45 V a vnitřním odporu
Ri = 2,25 Ω při daném osvětlení
(slunečním světlem). Tyto články jsou připojeny k rezistoru o odporu R
= 9 Ω.
a) Jak musíme sestavit tyto
články, aby rezistorem o odporu R procházel maximální proud?
b) Určete maximální výkon,
který mohou tyto články dodat rezistoru.
Předpokládejte, že v obou
případech jsou tyto články osvětleny slunečním světlem.