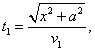
a čas potřebný k proběhnutí dráhy CB vztahem
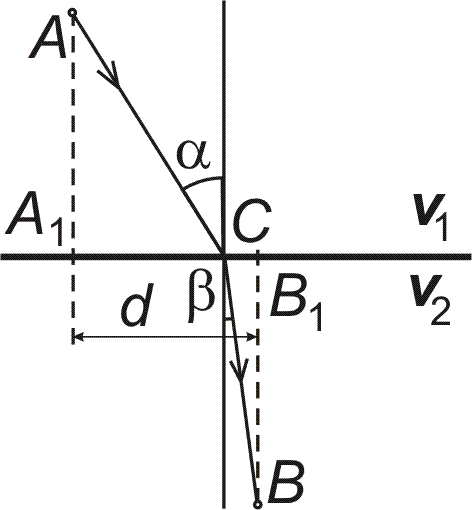
Řešení příkladu č. 8
| Předpokládejme, že světelný paprsek bude postupovat
cestou ACB, kde C je bod ležící na společném rozhraní
obou prostředí. Když si tento bod zvolíme za počátek pravoúhlé
souřadnicové soustavy s osou x v rozhraní, bod A bude mít
souřadnice [x, a] a bod B souřadnice [d - x,
b], pokud jsme stálou vzdálenost paty kolmice A a B,
tj. vzdálenost A1B1 označili d.
Jsou-li rychlosti světla v jednotlivých prostředích v1,
v2, čas potřebný k proběhnutí dráhy AC je daný
vztahem
a čas potřebný k proběhnutí dráhy CB vztahem
|
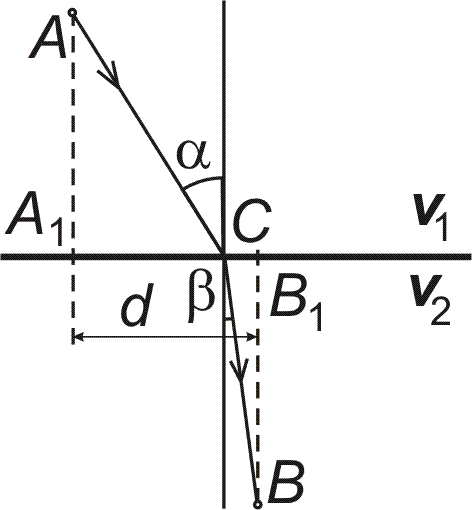 |
Celkový čas
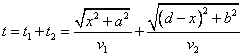
má být minimální, bude-li splněno
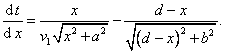
Hledáme minimální dobu, a proto položíme
![]()
z čehož
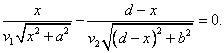
Z obrázku je zřejmé, že
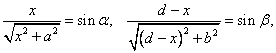
kde a, β představují úhly, pod kterými světelný paprsek dopadá na rozhraní, resp. se na něm láme.
Po dosazení dostáváme
![]()
což je zákon lomu.
Nyní ještě musíme pomocí druhé derivace ověřit, zda jsme skutečně našli lokální minimum.
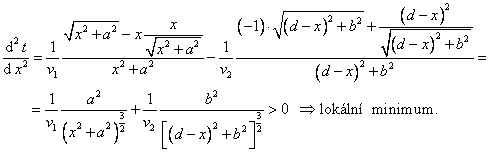
Světlo při přechodu z jednoho prostředí do druhého projde v nejkratší době dráhu splňující podmínky zákona lomu.