[Návrat do menu derivace]
Cvičení 7

Užití maxima a minima

Hledání maxima a minima na intervalu - obecný postup řešení úloh

  1. Zavedeme proměnné a přiřadíme jim symboly.

  2. Vyjádříme veličinu, jejíž maximum nebo minimum budeme hledat, pomocí těchto proměnných.

  3. Zjistíme vztahy mezi proměnnými ze zadání problému, abychom je mohli převést všechny na jedinou proměnnou.

  4. Vyjádříme veličinu, která se má maximalizovat nebo minimalizovat pomocí jediné proměnné.

Poznámka: proměnnou ve 3. kroku se snažíme zvolit tak, aby funkční závislost ve 4. kroku byla co nejjednodušší.

Příklad 1 - ilustrace předchozích zásad

     Jaký je nejekonomičtější tvar válcové konzervy s daným objemem, tj. jaký je nejmenší povrch (včetně víka a dna)?

Řešení:

  1. Označíme r poloměr a h výšku válce.
  2. Obsah povrchu je S = 2πr2 + 2πrh = 2π(r2 +  rh).
  3. Proměnné r, h jsou vázány vztahem V = πr2h, kde V je objem válce.
  4. Z této rovnice vyjádříme h:

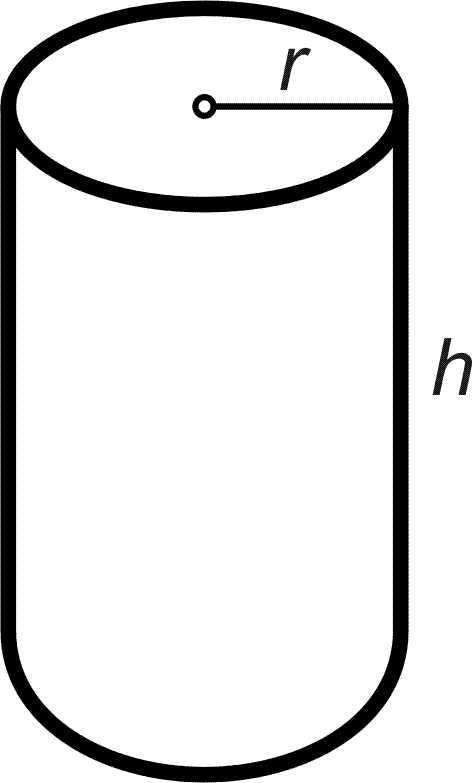         Potom

         Nyní jsme už úlohu převedli na matematický problém: najít minimum funkce S na intervalu r > 0.

Určíme derivaci funkce S:

Položíme S´ = 0, pak

Zda se jedná o lokální maximum nebo minimum, zjistíme pomocí druhé derivace:

Je tedy

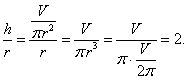
Optimální tvar tedy je h = 2r.

Další úlohy už jsou určeny k procvičování.

Příklad 2

Město B je ve vzdálenosti d = 10 km východně od města A a město C je     h = 3 km jižně od B (viz obrázek níže).  Z A do C se má postavit dálnice. Cena při budování dálnice podél existující silnice z A do B je 4 milióny Kč na km, zatímco cena kdekoli jinde je 5 miliónů na km. Kam by se měl umístit bod P, aby se minimalizovaly náklady?

Řešení

 

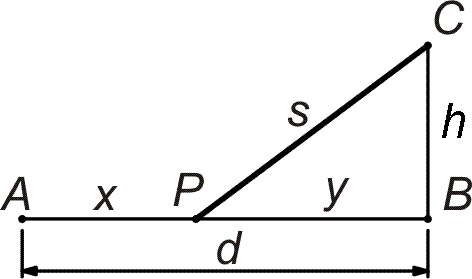Příklad 3

 a) Najděte rozměry obdélníka o obsahu 25, jehož obvod je minimální.

 b) Který obdélník s obvodem 20 má největší obsah?

Řešení

 

Příklad 4

Drát délky l =12 cm se rozdělí na dva kusy, z nichž první se ohne do kružnice a druhý do čtverce. Ukažte, že součet obou obsahů má minimální hodnotu 36/(4 + π) cm2; té se dosáhne tím, že strana čtverce je rovna průměru kružnice.

Řešení

 

Příklad 5

Drát délky l = 12 cm se má ohnout do tvaru obdélníka, na kterém pokračuje polokružnice (viz obr. vpravo). Ukažte, že maximální obsah je 72/(4 + π) cm2; toho se dosáhne, když poloměr kružnice je roven menší straně obdélníka.

Řešení

 

Příklad 6

Drát délky

se rozdělí na dva kusy, přičemž z jednoho se vyrobí čtverec a z druhého rovnostranný trojúhelník. Jaké by měly být délky kusů, aby součet obsahů byl minimální?

Řešení

Příklad 7

Najděte nejkratší možnou délku žebříku opřeného o svislou stěnu a o zem, který vede nad přístřeškem vysokým 8 m a postaveným 3 3/8 m od stěny (viz obrázek vpravo).

Řešení

 

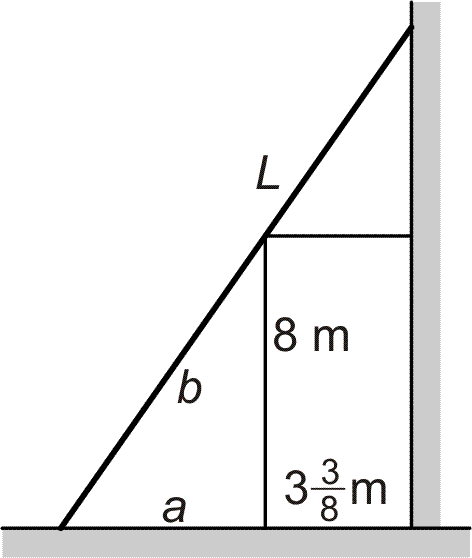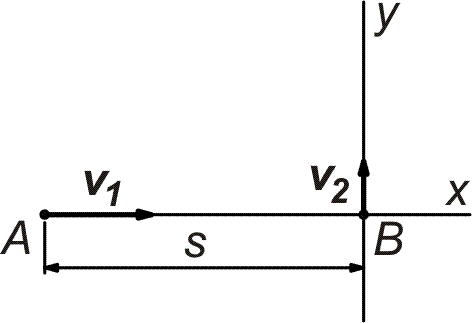
Příklad 8

 Ve čtyři hodiny odpoledne vyjelo auto A rychlostí 60 km/h ke křižovatce vzdálené 125 km na východ. Auto B jede na této křižovatce rychlostí 30 km/h na sever. Kdy budou tato auta nejblíže k sobě a jaká bude mezi nimi vzdálenost?      

Řešení