[Zpět na stránku Matematika křivek]

Logaritmická spirála

Historie a užití

Matematický popis spirály

Rovnice logaritmické spirály má v polárních souřadnicích tvar

kde r je poloměr - velikost vektoru spojujícího pól spirály a bod P ležící na spirále, a, b jsou konstantní parametry. Pokud bychom tuto rovnici zlogaritmovali, dostaneme

Z tohoto vztahu pak vznikl název "logaritmická spirála".

Parametrická rovnice

Rovnici logaritmické spirály je možno také vyjádřit parametricky

což je tvar vhodný pro vykreslení spirály pomocí počítače.

Pro hodnoty b ® 0 se bude spirála blížit kružnici (pro b = 0 vznikne kružnice). Změnu poloměru můžeme vyjádřit pomocí derivace

Z toho vyplývá, že nárůst spirály závisí pouze na hodnotě b, hodnota a určuje vzdálenost počátku spirály od jejího pólu.

Tečna v bodě logaritmické spirály svírá s průvodičem úhel θ, pro který platí

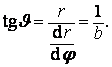
Protože parametr b je konstantní, můžeme říci, že logaritmická spirála je křivka, jejíž tečna svírá s touto křivkou stále stejný úhel, což se v praxi využívá např. při konstrukci řezných nástrojů.

Délka logaritmické spirály je konečná. Ukážeme si postup, jak ji můžeme určit.

Na spirále zvolíme libovolný bod A, jehož poloha je dána polárními souřadnicemi r, θ. Délku spirály od jejího počátku o souřadnicích r = a, φ = 0 až do bodu A určíme užitím vztahu pro výpočet délky pomocí parametrických rovnic, tj.

kde t je parametr. Potom

Abychom mohli dosadit do vztahu (14) pro výpočet délky křivky v parametrickém vyjádření, určíme ještě

Dále budeme dosazovat do vztahu (14)

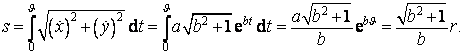
Konstrukce logaritmické spirály

Budeme-li postupně polárnímu úhlu přiřazovat hodnoty, které tvoří aritmetickou posloupnost, bude průvodič nabývat hodnot, které tvoří geometrickou posloupnost, tj.

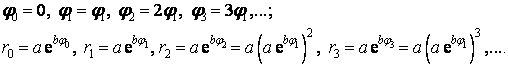
Vezmeme např.

a vypočteme příslušné hodnoty průvodiče, tj.

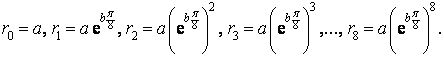
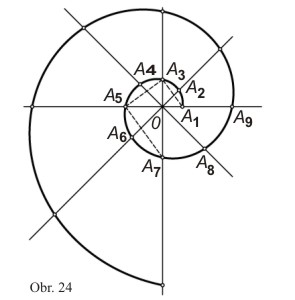
     Když jsme tedy rozdělili úhel φ = π na osm stejných částí a nanesli na příslušné polopřímky úsečky odpovídající hodnotám průvodiče, dostaneme prvních devět bodů spirály (obr. 24).

     Konstrukci dalších bodů lze provést geometricky. Všimněme si, že např.

tj. průvodič, který odpovídá úhlu

je geometrickým průměrem průvodičů r₀ a r₈, které odpovídají úhlům φ₀ = 0 a φ₈ = π. Úsečky A₁A₃  a  A₃A₅ jsou tedy navzájem kolmé.Vedeme-li nyní kolmici bodem A₅, dá její průsečík s přímkou OA₃ bod A₇, který náleží spirále, protože

neboli

Průsečík kolmice bodem A₇ na úsečku A₅A₇ s polární osou dá bod A₉ spirály, atd.

Takto můžeme sestrojit libovolný počet bodů spirály, ležících na vzájemně kolmých přímkách. Pro přesnější zakreslení grafu spirály je třeba ještě sestrojit řadu bodů, které budou ležet mezi dosud sestrojenými body.

             Sestrojíme-li dostatečné množství bodů a spojíme je plynulou čarou, dostaneme křivku odpovídající logaritmické spirále, jak je znázorněna na obr. 24.