[Zpět na stránku Matematika křivek]

 Cassiniho ovály

Z dnešního hlediska lze říci, že Cassiniho ovál je určitou analogií elipsy, a proto si kapitolu o kuželosečkách ještě doplníme o informaci i těchto křivkách.

Historie

Cassiniho ovál

      Jsou-li F₁ a F₂ dva různé pevně dané body v rovině, pak množina všech bodů X v rovině takových, že součin

kde k je konstantní se nazývá Cassiniho ovál.

V dalším postupu si ukážeme, jak z této formulace lze odvodit rovnici popisující Cassiniho ovál a Bernoulliho lemniskátu.

Označíme-li vzdálenost mezi body F₁ a F₂  (ohnisky) 2e, pak můžeme rovnici (17) přepsat na tvar

neboli

Po jednoduchých úpravách dostaneme

Nyní provedeme diskusi řešení rovnice (18) - tu už Cassini neprovedl. Diskusi provedeme tak, že určíme souřadnice průsečíků nejprve s osou x a potom s osou y.

a) Průsečíky s osou x : y = 0. Potom po dosazení do rovnice (18) dostaneme

což je kvadratická rovnice v proměnné x². Jejím řešením dostaneme

Po odmocnění dostaneme

b) Průsečíky s osou y : x = 0. Potom po dosazení do rovnice (18) dostaneme

což je kvadratická rovnice v proměnné y². Jejím řešením dostaneme

Po odmocnění dostaneme

Z uvedených vztahů je vidět, že některé průsečíky by mohly být imaginární.

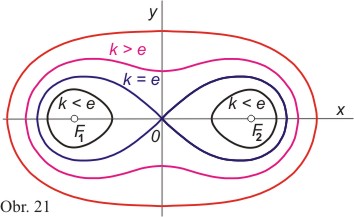
Je-li e > k, potom neexistují průsečíky s osou y v R; z toho vyplývá, že v tomto případě Cassiniho křivka není souvislá, bude se skládat ze dvou větví.

Je-li e < k, je Cassiniho ovál souvislá křivka.

Je-li e = k, potom Cassiniho křivka má s osou x jediný průsečík (křivka prochází počátkem soustavy souřadnic a protíná sebe sama), potom rovnice (18) přejde na tvar

což je tzv. Bernoulliho lemniskáta.