Délka křivky
Příklad 9 (asteroida)
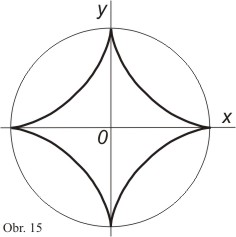Určete
délku asteroidy (obr. 15). Tato křivka má parametrické rovnice
Řešení
Protože asteroida je symetrická vzhledem k oběma souřadnicovým osám, stačí vzít délku jedné její čtvrtiny v 1. kvadrantu, tj.
Dále použijeme vzorec (14), kam dosadíme za
Délka celé asteroidy je tedy s = 6a.
Příklad 10 (kardioida)
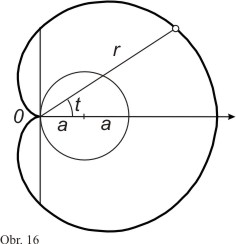
Určete délku kardioidy (obr. 16), jejíž rovnice je dána pomocí polární soustavy souřadnic
Řešení
K vyřešení úlohy použijeme vztahu (16). Protože kardioida je symetrická podle osy x, lze psát
Příklad 11 (cykloida)
Určete délku oblouku cykloidy dané parametrickými rovnicemi
Řešení
Použijeme vzorec (14), kam dosadíme za
Ze symetrie
dále použijeme vzorec
Po dosazení a úpravě je
Příklad 12 (elipsa)
Určete délku elipsy dané parametricky (a < b)
Řešení
Budeme postupovat obdobně jako v předchozím příkladu. Vzhledem k symetrii elipsy můžeme psát
Označíme-li
Potom můžeme psát
Červeně označený výraz je úplný eliptický integrál 2. druhu. (Tento integrál nelze určit běžnými metodami, řeší se numericky, jeho hodnoty jsou tabelovány.) Z řešení této úlohy je vidět, že ne vždy jsme schopni provést výpočet délky křivky běžnými metodami integrace - toto je jedna z těch úloh, která vedla k zavedení tzv. eliptických integrálů.