Křivka a její rovnice
Nechť je křivka dána svojí geometrickou vlastností (tj. jako geometrické místo bodů). Tuto křivku budeme vyšetřovat jako trajektorii pohybu bodu M, který má proměnné souřadnice R, φ. (V řadě případů se ukazuje výhodné pracovat pomocí polárních souřadnic.) Potom bude muset geometrické vlastnosti, kterou je křivka určena, odpovídat analytický vztah mezi souřadnicemi R a φ, který je právě rovnicí křivky. V obecném případě je možno psát rovnici křivky v polárních souřadnicích ve tvaru
a uvažovat R jako funkci úhlu φ.
Je zřejmé, že je-li naopak zadána funkce
geometricky se znázorní křivkou.
Shrneme-li výše uvedenou úvahu, můžeme říci, že křivce dané geometrickou vlastností odpovídá rovnice
a naopak, že rovnici
odpovídá křivka. Z toho pak vznikají dva typy úloh:
a) je dána křivka jako geometrické místo bodů; sestavte rovnici této křivky;
b) je dána rovnice mezi souřadnicemi R a φ; sestrojte křivku, která je vyjádřena touto rovnicí.
Ukažme si to na následujícím příkladu.
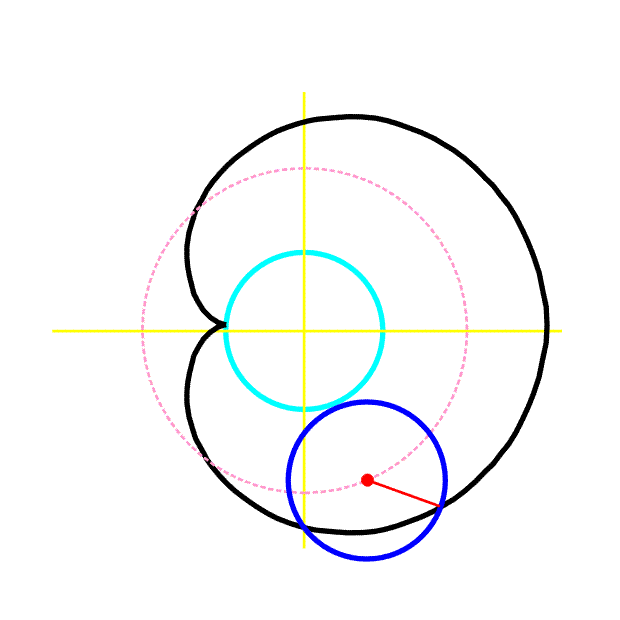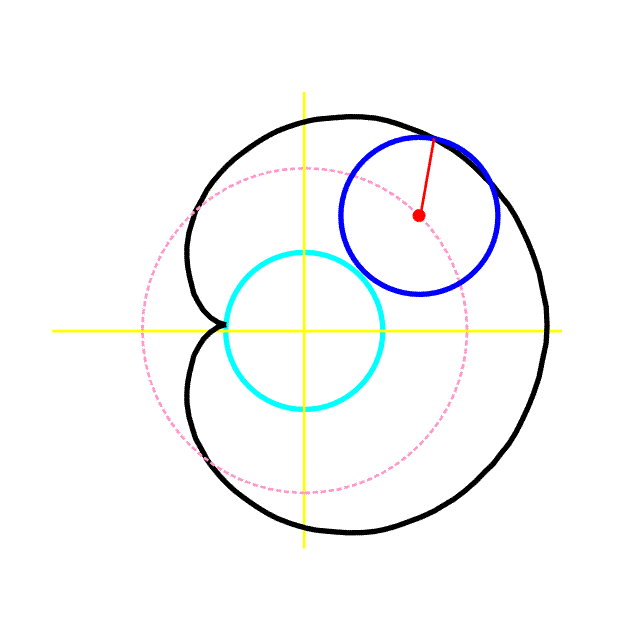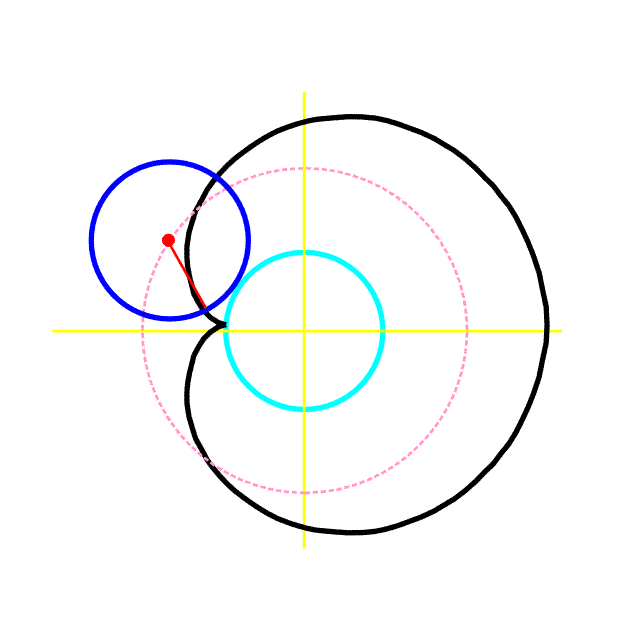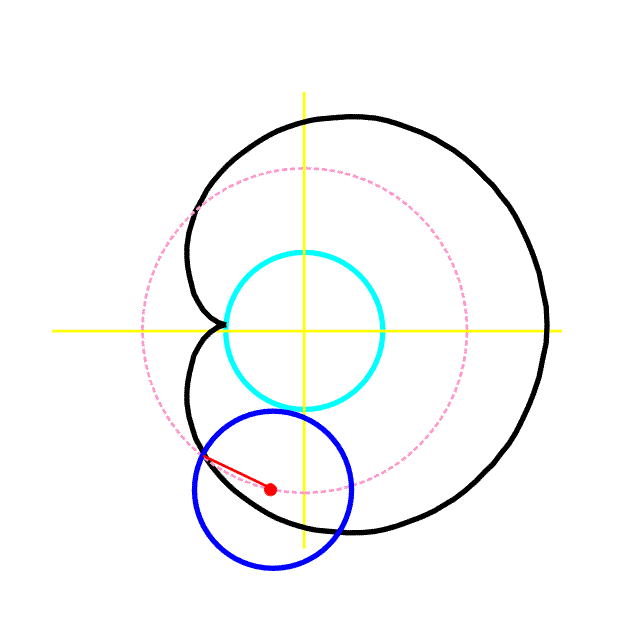
Příklad 6 (kardioida)
Kružnice o poloměru a se valí bez prokluzu po pevné kružnici téhož poloměru a.
a) Napište rovnici křivky, kterou opisuje bod M (obr. 8) ležící na obvodu pohybující se kružnice.
b) Určete tvar kardioidy.
Řešení
a)
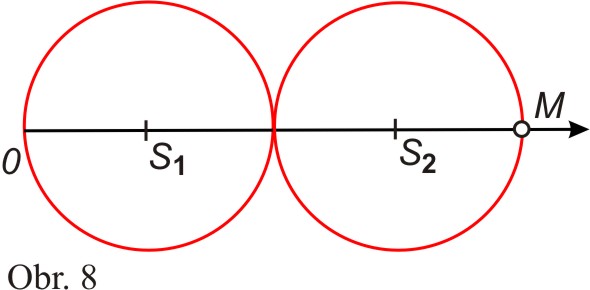Na
obr. 8 je zobrazena počáteční poloha odvalující se kružnice. Polární osu a
pól zvolíme podle obr. 8. Po určité době pohybu se poloha bodu M
změní tak, jak je znázorněno na obr. 9.
Vyšetříme vztah mezi délkami oblouků NAO a NBM. Je zřejmé, že bod M padne do pólu O, když pohybující se kružnice obejde polovinu obvodu pevné kružnice. To znamená, že délka oblouku na obvodu pohybující se kružnice od bodu N, který je bodem dotyku obou kružnic, k bodu M se rovná délce oblouku na obvodu pevné kružnice od téhož bodu N k pólu.Protože poloměry obou kružnic jsou stejně velké, jsou i středové úhly
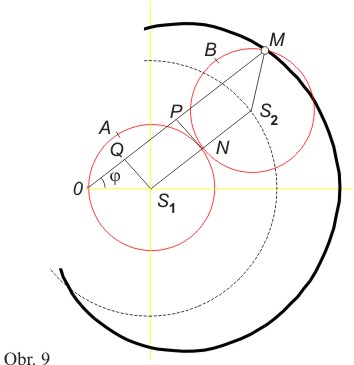
Útvar OS1S2M tedy tvoří rovnoramenný lichoběžník, a proto jsou úsečky S1S2 a OM (|OM| = R) rovnoběžné. Spustíme-li kolmici z bodu N na úsečku OM, můžeme psát |OP| = |PM|, a tedy R = 2|OP|.
Protože |OP| = |OQ| + |QP| a |OQ| = a cos φ, |QP| = |S1N| = a, najdeme
neboli
Toto je tedy hledaná rovnice kardioidy.
b)
Nalezenou rovnici nyní použijeme k určení tvaru kardioidy. Pro φ = 0 je R = 4a. Bod M leží na polární ose ve vzdálenosti 4a od pólu (počáteční poloha).
Položíme-li
Pro hodnotu
tj. bod M splyne s pólem. Pro hodnotu
Pro další změny úhlu φ opíše bod M zbývající část křivky, při hodnotě φ = 2π se vrátí do původní polohy a dále bude pokračovat v pohybu po téže křivce.
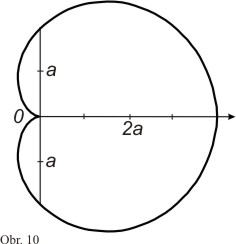
Dále bychom mohli ještě dopočítat několik dalších hodnot R odpovídajících zvolenému úhlu φ. Dále bychom pak sestrojili příslušné body a proložili jimi souvislou křivku, jak je znázorněno na obr. 10.
Výše uvedená křivka se obecně nazývá epicykloida. Při různých vztazích mezi poloměry pohyblivých a pevných kružnic dostáváme různé epicykloidy. Kardioida tedy patří mezi epicykloidy - je to taková epicykloida, kterou dostaneme v případě rovnosti poloměrů pohybující se i pevné kružnice.
Poznámka: