Polohu bodu v prostoru je možno určit pomocí kartézské soustavy souřadnic. V této soustavě souřadnic je poloha bodu dána trojicí souřadnic x, y, z, např. na  obr. vpravo je poloha bodu A dána jako trojice souřadnic, tj. A = [x, y, z] anebo je možno polohu bodu A zadat v této soustavě souřadnic pomocí tzv. polohového vektoru r.      Polohový vektor r je vektor, který má počáteční bod v počátku soustavy souřadnic a koncový bod v bodě A.      Abychom mohli lépe popsat polohu bodu A pomocí polohového vektoru, je vhodné zavést ve směru souřadnicových os jednotkové vektory i, j, k, pro které platí | i | = | j | = | k | = 1.

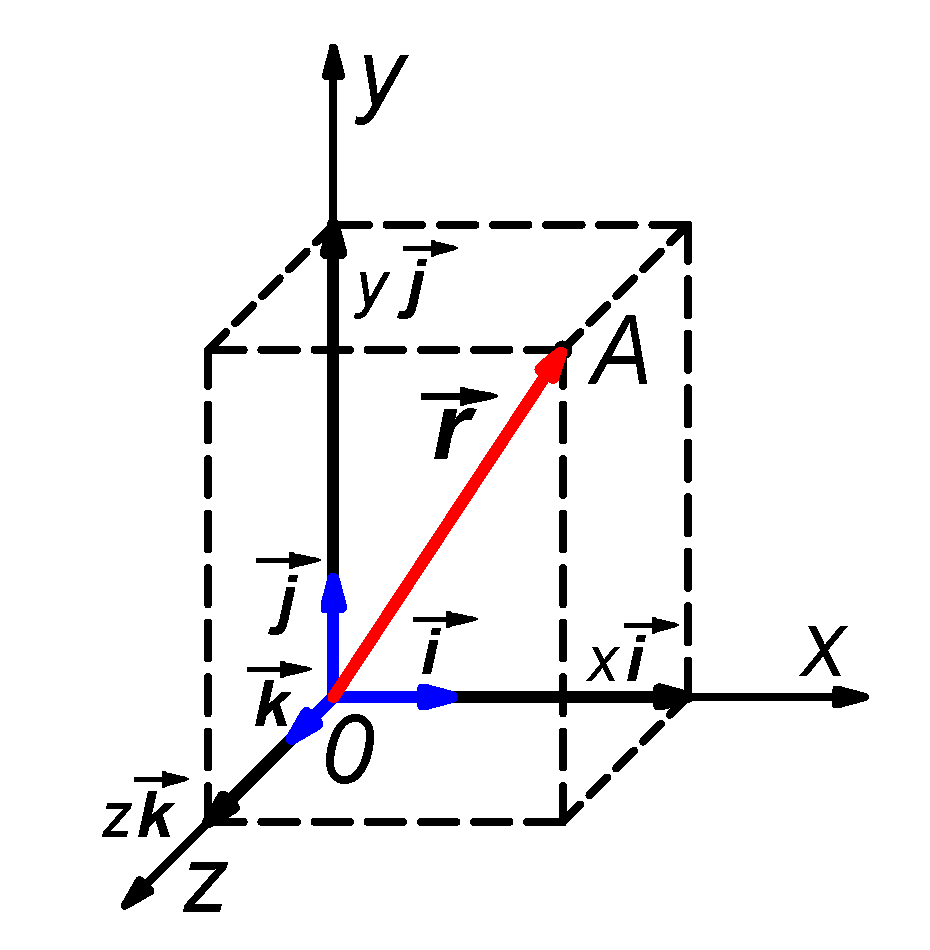         Polohový vektor pak můžeme získat složením násobků těchto vektorů souřadnicemi x, y, z, tj.

                     r = x i + y j + z k.

      Připomeňme pouze, že tučná písmena nám v tomto textu nahrazují veličiny označené v běžně psaném textu šipkou (vektory), jak je použito i na obrázku vpravo.

     Protože polohový vektor je funkcí souřadnic x, y, z, můžeme také stručně psát         r = r (x, y, z).       

     Velikost polohového vektoru r  v prostoru  můžeme vypočítat pomocí Pythagorovy věty

Nyní se podíváme, jak polohový vektor derivovat. Zatím víme, že v případě volného pádu jsme odvodili, že okamžitá rychlost se určí jako časová změna funkce (v tomto případě je funkcí uražená dráha - změna y-ové souřadnice):

Při pohybu tělesa nebo hmotného bodu se obvykle ale nemění pouze jedna souřadnice, mohou se měnit všechny tři, neboli jinak řečeno - mění se poloha tělesa - polohový vektor tělesa.

     S použitím zavedené symboliky se nyní pokusíme popsat změnu polohového vektoru r  v prostoru, čímž vlastně také určíme vektor okamžité rychlosti v. (Z technických důvodů aby bylo vše lépe patrné použijeme dále ve vzorcích zápis vektorů pomocí šipek.)

Derivaci polohového vektoru jsme zde vyjádřili pomocí tzv. diferenciálu funkce.

Výraz

je možno chápat jako naznačenou derivaci, kterou dále technicky provedeme. Při této realizaci použijeme pravidla pro výpočet  derivace součtu.

Další úpravu použijeme větu o derivaci konstanty (konstantu můžeme vytknout před derivaci).

Výše uvedeným postupem jsme vlastně odvodili, že derivaci vektoru je možno nahradit derivací jeho složek. Tento postup často užíváme při řešení úloh. Rovnice

je vlastně zkrácený zápis  trojice rovnic

Velikost vektoru okamžité rychlosti je pak dána vztahem

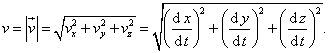
Shrneme-li naše úvahy ohledně okamžité rychlosti, což byl příklad časové změny polohového vektoru, můžeme říci, že vektor okamžité rychlosti lze zapsat analogickým způsobem, jako polohový vektor, tj.

Podobným způsobem pomocí složek bychom mohli popsat jakoukoli změnu jiné vektorové veličiny, např. zrychlení:

což je opět zkrácený způsob zápisu pro tři složkové rovnice