Jedním z úkolů při vyšetřování průběhu funkce je nejen sestrojení grafu funkce, ale i zjištění některých základních vlastností funkce, které by mohly zjednodušit postup při kreslení grafu funkce.

     Při konstrukci grafu je vhodné se řídit níže uvedeným (zjednodušeným) schématem vyšetřování průběhu funkcí:

1. Určíme definiční obor funkce, spojitost funkce, vlastnosti funkce: např. sudá, lichá..
2. Najdeme hodnoty argumentu, pro který má funkce extrémy.
3. Nalezneme hodnoty x, pro které má graf funkce inflexní body.
4. Vypočteme hodnoty funkce y = f(x), které odpovídají všem takto určeným hodnotám argumentu x. Takto získáme souřadnice "opěrných"  bodů grafu funkce. Abychom dosáhli větší přesnosti konstrukce grafu funkce, můžeme přibrat ještě některé jiné body, např. průsečíky grafu s osami souřadnic.
5. Určíme intervaly, kdy je daná funkce rostoucí nebo klesající.
6. Určíme intervaly, kdy je daná funkce konvexní (konkávní).
7. Sestrojíme v náčrtku všechny určené body a narýsujeme graf, přičemž dbáme na poznámky vztahující se k první a druhé derivaci dané funkce.

Grafy funkcí je možno např. pro kontrolu správnosti postupu také modelovat na počítači pomocí programu, který je volně k dispozici ke stažení na Internetu: Matmat.

Podrobnější schéma pro vykreslování grafů funkcí a další příklady (které již nejsou vzhledem k fyzikálnímu zaměření tohoto textu dále uváděny) je možno nalézt např. v učebnici matematiky:

Hrubý D., Kubát, J.: Matematika pro gymnázia (Diferenciální a integrální počet), Prometheus, Praha 1997.

Příklad (ukázka, jak vyšetřovat průběh funkce):

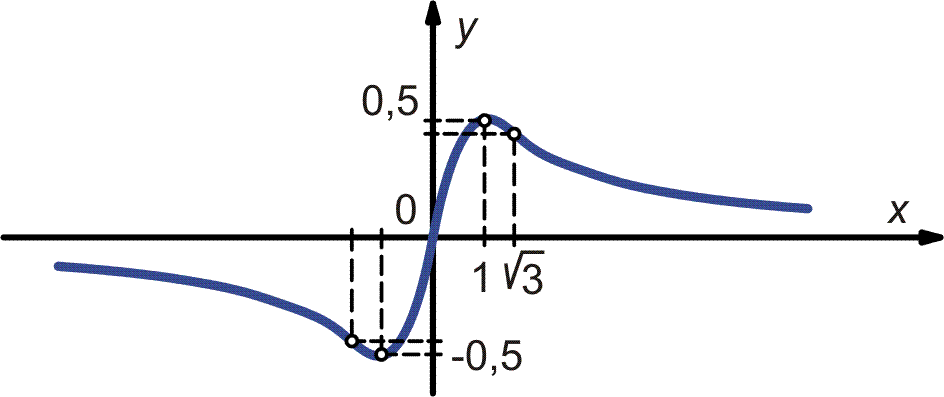
     Vyšetřete průběh funkce a načrtněte graf  této funkce

Řešení:

1. D(f) = (- ¥ ; +¥), funkce je spojitá v celém definičním oboru, protože platí f(-x) = - f(x) je daná funkce lichá.

2. Lokální extrémy funkce

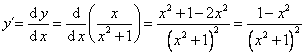
          Hledáme taková x, pro která je y´= 0, tj. musí platit:

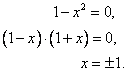
          V bodech x = - 1, x = +1 mohou tedy nastat lokální extrémy. Nyní musíme tyto body dále vyšetřit pomocí druhé derivace:

         Po dosazení za x = -1, x = +1 do druhé derivace dostaneme

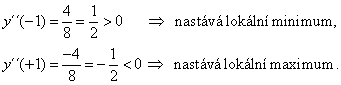
        3. Inflexní body: y´´ = 0.

        4. Funkce prochází bodem [0; 0]. Dále je možno ještě určit limity v nekonečnu zprava a zleva.

        5. Určíme intervaly, kdy je daná funkce rostoucí nebo klesající:

       6. Určíme intervaly, kdy je funkce konvexní nebo konkávní:

       7. Graf funkce