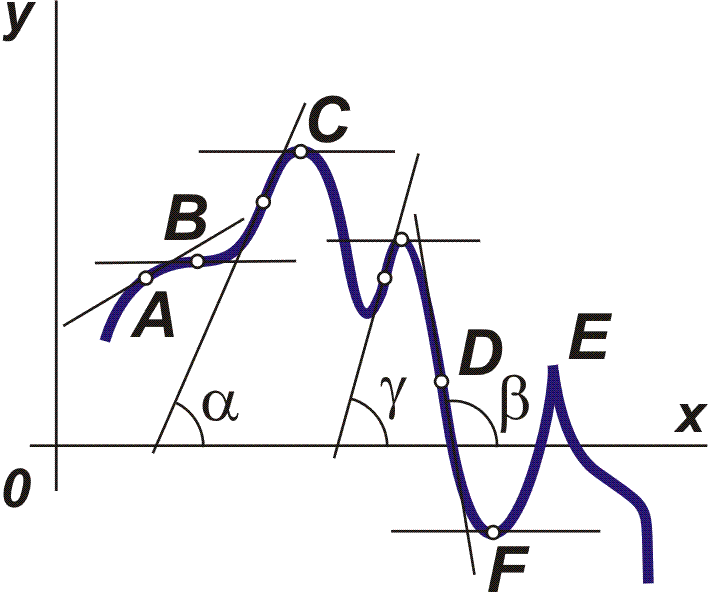
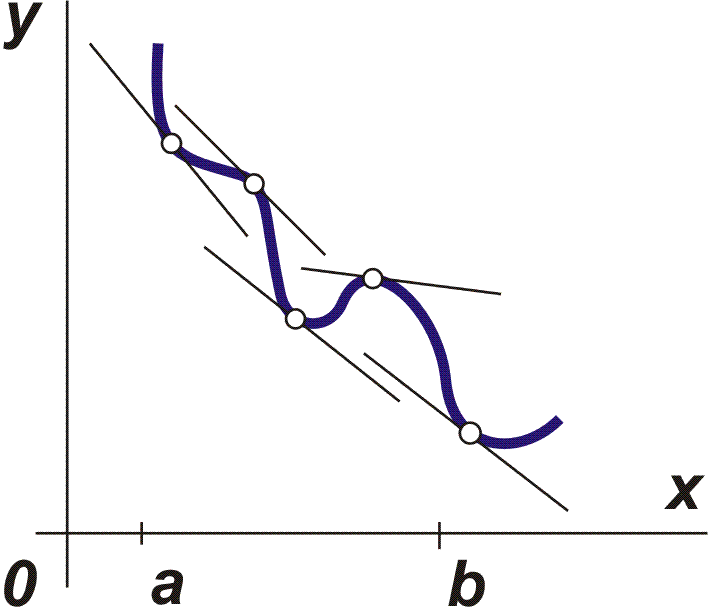
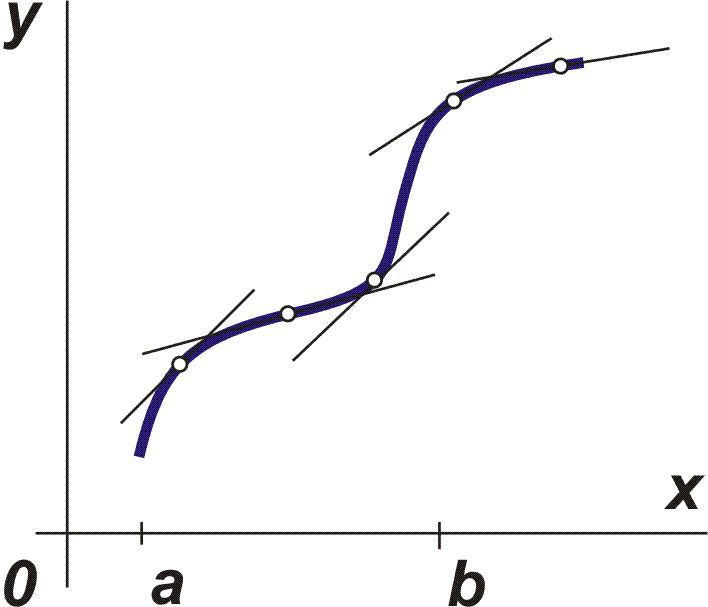
Budeme uvažovat, že máme funkci f(x), kterou na daném intervalu zobrazíme jako nějakou spojitou (tj. nepřerušenou) křivku (viz obr. vpravo).      Každou takovou funkci budeme nazývat spojitou funkcí. Hodnota derivace (pokud existuje) v libovolném bodě takové křivky určuje velikost směrnice tečny, tj. tg a = f ´(x) v daném bodě (viz obr. vpravo), a pak nazýváme směrový úhel příslušné tečny.      Je-li 0 < a < 900 , pak f ´(x) > 0. Funkce splňující na daném intervalu tuto podmínku nazýváme funkcí rostoucí.      Je-li 900 < a < 1800 , pak f ´(x) < 0. Takovou funkci nazýváme na daném intervalu funkcí klesající.

Je-li funkce na daném intervalu rostoucí nebo klesající, říkáme, funkce je na tomto intervalu monotónní.

Kromě výše popsaných případů ještě může nastat situace, že první derivace funkce f(x) je v rámci daného intervalu rovna nule, tj. f ´(x) = 0. Pak musíme rozlišit několik možností: funkce může mít buď lokální extrémy - lokální maximum (v bodě C na prvním obrázku), lokální minimum (bod F) nebo může mít tzv. inflexní bod (např. body D nebo E, nebo i další nepopsané? - zkuste je na prvním obrázku nalézt) - jsou to body, ve kterých funkce mění "znaménko poloměru zakřivení na opačné", jinak řečeno funkce konvexní se mění na funkci konkávní a naopak.

Zbývá nám ještě vysvětlit, jak je to s bodem E: tam je vlastně ostrá špička - což znamená, že funkce je tam sice spojitá, ale neexistuje v tomto bodě derivace.

Obecně můžeme říci, že je-li funkce na daném intervalu spojitá, ještě nemusí ve všech bodech tohoto intervalu existovat derivace této funkce. Ovšem opačně platí, má-li funkce ve všech bodech intervalu derivaci, je v tomto intervalu spojitá.

Dále se už zaměříme na to, jak zjistit  pro f ´(x) = 0, který z výše popsaných případů nastane.

Poznámka 1:

     V mnoha případech nemusíme rozhodnutí, zda je v daném bodě a v případě f ´(a) = 0 lokální maximum nebo minimum, provádět dalším derivováním funkce. Často si stačí jen uvědomit následující poznatky:

• je-li pro x  < a spojitá funkce rostoucí a pro x > a klesající, pak je zřejmě v bodě a lokální maximum,
• je-li pro x < a spojitá funkce klesající a pro x < a rostoucí, pak je zřejmě v bodě a lokální minimum,
• je-li pro x < a spojitá funkce rostoucí (klesající) a pro x > a opět rostoucí (klesající), pak je zřejmě v bodě a inflexní bod.

Poznámka 2:

     Budeme-li u dané funkce uvažovat i krajní body intervalu, můžeme u dané funkce určovat tzv. globální extrémy. Tam je třeba si uvědomit, že získané lokální extrémy je třeba ještě navíc porovnat s krajními body a teprve pak rozhodnout, co je vlastně globálním ("celkovým") extrémem dané funkce.