Nerovnoměrný pohyb a jeho rychlost
![]()
V předchozí části Rovnoměrný pohyb a jeho rychlost jsme zavedli pojem rychlosti jakéhokoli rovnoměrného postupu změn. Avšak děje, které je možno pozorovat v přírodě jsou většinou nerovnoměrné. Stačí jen vyšetřovat volný pád vlivem tíhového pole.
 |
Z fyziky víme, že volný pád tělesa ve vakuu je popsán
vztahem
kde t je doba od začátku pádu, s je dráha uražená za dobu t a g je tíhové zrychlení. Tento pohyb je nerovnoměrný. Nyní chceme vyšetřit problém definice rychlosti nerovnoměrného průběhu změny. Vyšetřování tohoto problému začneme úlohou stanovit rychlost nerovnoměrného pohybu. Abychom si lépe ujasnili postup našeho uvažování, zůstaneme u příkladu volného pádu hmotného bodu ve vakuu. Určili jsme, že rychlost rovnoměrného pohybu je definována jako
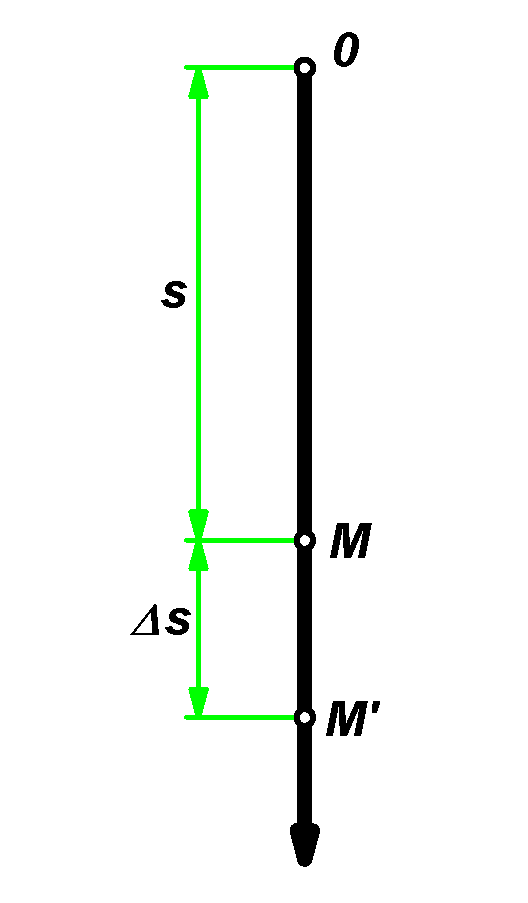
I při zkoumání otázky pojmu rychlosti nerovnoměrného pohybu se pokusíme vyjít z tohoto vztahu. Uvažujme určitý okamžik doby t. Předpokládejme, že se hmotný bod nalézá v tomto okamžiku v poloze M (viz obr.). Velikost dráhy s = OM, uražené hmotným bodem za dobu t, se určí ze vzorce (6):
|
Předpokládejme, že v okamžiku t + Δt bude hmotný bod zaujímat polohu M' . Přírůstek dráhy MM', odpovídající časovému intervalu Δt, označíme Δs. Dosazením veličiny t + Δt do vzorce (6) místo t, obdržíme pro novou hodnotu dráhy OM' výraz
![]()
Odečteme-li od této rovnice rovnici (6), nalezneme Δs:
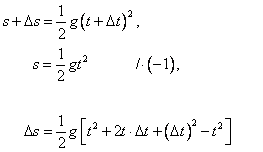
čili
![]()
Dělíme-li Δs číslem Δt, obdržíme výraz, který určuje Δs/Δt :
![]()
čili po zkrácení zlomku číslem Δt :
![]()
Shrnutí
Při rovnoměrném pohybu je poměr Δs/Δt, který definuje rychlost pohybu, veličina konstantní; zůstává nezměněna při libovolné hodnotě t a libovolné hodnotě Δt. Proto je možno užít při odvozování velikosti rychlosti rovnoměrného pohybu libovolný okamžik t a libovolný přírůstek Δt.
Při nerovnoměrném pohybu tomu tak není. Na příkladu volného pádu hmotného bodu vidíme, že podíl Δs/Δt závisí jak na t, tak i na Δt. Při téže hodnotě Δt odpovídají různým okamžikům t různé hodnoty podílu Δs/Δt .
Příklad: při Δt = 0,1 s v okamžiku t = 1 s je
![]()
v okamžiku t = 3 s tomu odpovídá hodnota
![]()
Proto je možno vztahovat pojem rychlosti nerovnoměrného pohybu jen k určitému okamžiku. Není možno mluvit o rychlosti volného pádu hmotného bodu obecně, nýbrž jen o rychlosti, s jakou hmotný bod padá v daném okamžiku, tj. o okamžité rychlosti volného pádu.
[Pokračovat] [Zpět na stránku pojem derivace]