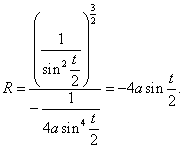Oskulační kružnice a poloměr křivosti
![]()
 Mějme
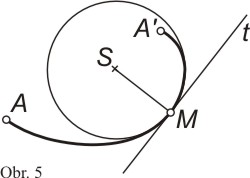
nějakou křivku AA', která má v bodě M
křivost rovnou K (obr. 5). Sestrojme tečnu a normálu křivky v bodě M.
Postupně budeme prokládat bodem M kružnice, jejichž středy budou ležet na
normále ve směru, kterým je křivka vydutá. Všechny tyto kružnice budou mít v
bodě M společnou tečnu s křivkou AA'; v
okolí bodu M jsou tyto kružnice vyduté týmž směrem jako křivka. Mezi
těmito kružnicemi existuje také taková kružnice, která bude mít stejnou křivost
K jako křivka v bodě M. Ze vztahu mezi křivostí a poloměrem
kružnice plyne, že poloměr zkoumané kružnice musí být roven absolutní hodnotě z
čísla 1/K.
Mějme
nějakou křivku AA', která má v bodě M
křivost rovnou K (obr. 5). Sestrojme tečnu a normálu křivky v bodě M.
Postupně budeme prokládat bodem M kružnice, jejichž středy budou ležet na
normále ve směru, kterým je křivka vydutá. Všechny tyto kružnice budou mít v
bodě M společnou tečnu s křivkou AA'; v
okolí bodu M jsou tyto kružnice vyduté týmž směrem jako křivka. Mezi
těmito kružnicemi existuje také taková kružnice, která bude mít stejnou křivost
K jako křivka v bodě M. Ze vztahu mezi křivostí a poloměrem
kružnice plyne, že poloměr zkoumané kružnice musí být roven absolutní hodnotě z
čísla 1/K.
Takto sestrojená kružnice se nazývá
oskulační kružnice křivky v bodě M.
Převrácená hodnota křivosti v bodě M, tj. hodnota R = 1/K,
se nazývá poloměr křivosti a střed S
oskulační kružnice středem křivosti křivky v
bodě M.
Podobně jako tečna charakterizuje stoupání křivky v daném bodě, oskulační kružnice dává názornou představu o zakřivení křivky v daném bodě. Můžeme tedy říci, že oskulační kružnice se přimyká křivce těsněji, než libovolná z ostatních kružnic, které se dotýkají křivky v daném bodě M a v malém okolí bodu M s velkou přesností nahrazuje přibližně křivku.
Vztah pro výpočet poloměru křivosti lze snadno odvodit z rovnice
![]()
kam za K dosadíme ze vztahu (4).
Potom je
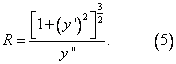
Výpočet středu křivosti
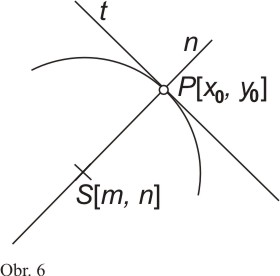
Při odvozování
vztahů pro výpočet souřadnic středu křivosti vyjdeme z poznatků, že střed
křivosti S leží na normále, která prochází bodem
P = [x0;
y0] kolmo k tečně. Pro vzdálenost |SP|
pak platí, že |SP| = R (obr. 6).
![]()
![]()
Protože bod S leží na normále n, můžeme psát
![]()
z čehož
![]()
Protože bod P[x0 ; y0] leží na oskulační kružnici se středem S[m; n], můžeme psát
![]()
Vztahy (6) a (7) představují soustavu dvou rovnic o dvou neznámých. Řešením této soustavy a po dosazení za R ze vztahu (5), dostaneme
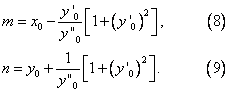
Příklad 2 (výpočet poloměru křivosti hyperboly)
Určete poloměr a souřadnice středu křivosti rovnoosé hyperboly dané rovnicí xy = 20 v bodě [4; 5].
Řešení:
Rovnici hyperboly přepíšeme do tvaru
![]()
Potom
![]()
Pro x = 4 dostaneme
![]()
Po dosazení do (5) dostaneme
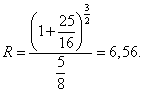
Střed křivosti má souřadnice, které určíme dosazením do (8) a (9)
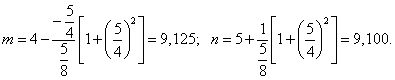
Příklad 3 (výpočet poloměru křivosti elipsy)
Určete poloměr a střed křivosti elipsy o rovnici
![]()
Řešení:
Jedná se o bod nad osou x, a proto
![]()
Určíme první a druhou derivaci funkce y. Dostaneme
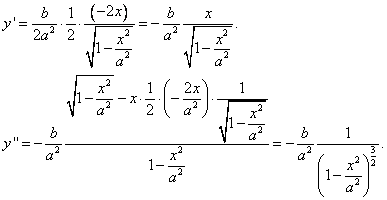
Pro x = 0 je
![]()
Po dosazení do (5) dostaneme
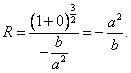
Souřadnice středu křivosti dostaneme po dosazení do (8) a (9)
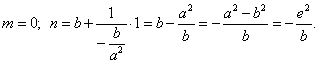
Příklad 4 (výpočet poloměru křivosti řetězovky)
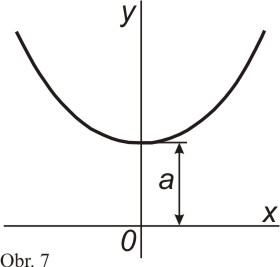
Křivku tvaru řetězovky vytvoří např. pružné, homogenní neroztažitelné lano zavěšené na dvou svých koncích (obr. 7).
Odvoďte obecný vztah pro výpočet středu a poloměru křivosti řetězovky dané rovnicí
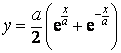
Řešení:
Určíme y' a y":
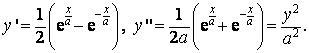
Dále vypočteme
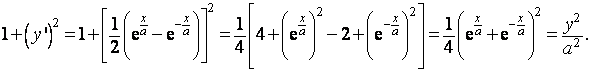
Potom
![]()
Po dosazení do (5) dostaneme
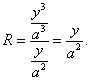
Souřadnice středu křivosti dostaneme po dosazení do rovnice (8) a (9)
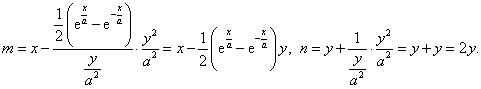
Např. pro x = 0 je y = a, m = 0, n = 2a, R = a.
Cykloida
Cykloida je křivka, kterou opíše určitý bod kružnice, která se valí (bez prokluzu) po pevné přímce. Parametrické rovnice cykloidy jsou dány vztahy
![]()
Cykloida je definovaná v intervalu (-∞, +∞), v dalších výpočtech ale musíme vyloučit body, t = 0, ±π, ..., ve kterých nejsou spojité derivace.
Příklad 5 (poloměr křivosti cykloidy)
Určete poloměr křivosti cykloidy v běžném bodě.
Řešení
Ve vzorci pro výpočet poloměru křivosti se vyskytují první a druhá derivace souřadnice y podle proměnné x. V parametrických rovnicích cykloidy jsou souřadnice x a y funkcemi parametru t. Máme-li však závislost mezi x a t, můžeme t považovat za funkci x (což můžeme udělat, protože funkce x = a(t - sin t) je v celém intervalu (-∞, +∞) spojitá rostoucí funkce a proto k ní také existuje funkce inverzní).
Proto můžeme derivovat y podle x, přičemž výraz (1 - cos t) považujeme za složenou funkci x. Dostaneme
![]()
Derivujeme-li rovnici x = a(t - sin t) podle x, nalezneme
![]()
Dosadíme-li tento výraz do vzorce pro výpočet y', dostaneme
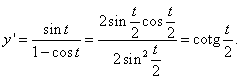
Derivací y' podle x dostaneme y"
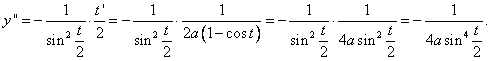
Dále vypočteme
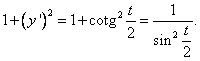
Po dosazení do (5) dostaneme