[Zpět na stránku matematika křivek]

Křivost křivky

Křivost křivky je jedním z prvků, které charakterizují křivku. Jinak řečeno je to také zakřivení křivky v různých bodech.

Při pohybu od jednoho bodu M křivky ke druhému bodu M' se bude současně také měnit poloha tečny ke křivce: tečna se bude otáčet. Toto odlišuje křivku od přímky, jejíž tečna s ní splývá ve všech jejích bodech - tedy přímka a tečna mají stejný směr. Čím větší bude úhel, o který se otočí tečna při přechodu z bodu M do bodu M' křivky, tím více se také bude lišit oblouk křivky od přímky a tím větší bude také zakřivení křivky.

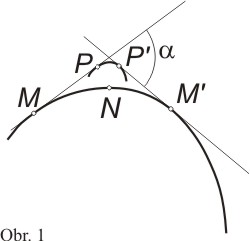
     Zakřivení oblouku však nelze charakterizovat jen úhlem, o který se otočí tečna křivky při přechodu z jednoho krajního bodu oblouku do druhého krajního bodu. Na obr. 1 jsou nakresleny dva oblouky - oblouk PP' a oblouk MM', jejichž zakřivení jsou různá, ale úhel, o který se otočí tečna je stejný. Z toho vyplývá, že chceme-li stanovit míru zakřivení oblouku dané křivky, je nutné uvažovat také jeho délku. Z obr. 1 je patrné, že při stejném úhlu, o který se otočí tečna, je zakřivení tím větší, čím kratší je délka oblouku.

     Ukazuje se jako přirozené definovat průměrnou křivost oblouku křivky jako poměr úhlu tečen v krajních bodech oblouku k délce oblouku, neboli jako úhel, o který se otočí tečna křivky na jednotkové délce oblouku:

kde úhel  α je vždy v obloukové míře.

     Ilustrujme si nyní výše uvedený postup na výpočtu průměrné křivosti kružnice o poloměru R.

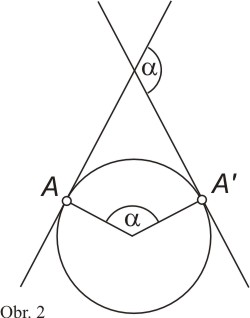
Pro každý oblouk kružnice je úhel α tečen ke kružnici v krajních bodech oblouku roven úhlu poloměrů v dotykových bodech (obr. 2). Délka oblouku AA'  je αR, takže průměrná křivost oblouku je stejná ve všech jeho částech a je rovna

 Dostali jsme, že průměrná křivost kružnice je převrácená hodnota poloměru a je tedy nepřímo úměrná poloměru kružnice.

     Na základě výše uvedených úvah můžeme tedy říci, že průměrná křivost charakterizuje celkové zakřivení oblouku.

     V různých částech oblouku ale může být zakřivení různé, což je vidět např. na obr. 1, kdy je část MN oblouku MM' více zakřivena než část NM'.

     Můžeme tedy říci, že průměrná křivost bude tím přesněji charakterizovat zakřivení oblouku křivky v různých bodech, čím menší bude délka oblouku. Analogickým postupem, jako se provádí přechod z rychlosti průměrné k rychlosti okamžité, lze tedy provést limitní přechod od křivosti průměrné ke křivosti v bodě, tj. pro křivost K můžeme psát

V dalším postupu odvodíme vzorec pro výpočet křivosti K v bodě. Předpokládejme, že křivka je dána rovnicí

Budeme-li hledat křivost v bodě, musíme kromě křivky ještě znát souřadnice této křivky. To znamená, že máme-li odvodit vzorec pro výpočet křivosti K, potřebujeme vyjádřit limitu

Toto vyjádření musíme provést pomocí souřadnic x a y bodu M křivky, přičemž y = f(x).

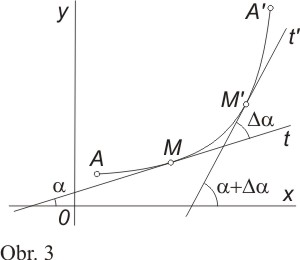
Předpokládejme, že M = [x; y]. Zvětšíme-li x o přírůstek Δx, pak hodnotě úsečky x + Δx přísluší bod M' křivky. V bodech M a M'  veďme tečny t a t'  (obr. 3).

Označíme-li α úhel, který svírá tečna t s osou x v bodě M, změní se při přechodu M ® M' úhel α na úhel α + Δα. Přírůstek Δα je zároveň i úhlem, o který se otočí tečna.

Označíme-li oblouk

pak je

Pak platí

Tento výraz můžeme upravit na

Pro s' můžeme odvodit vztah

Obdobně nyní odvodíme i vztah pro α'. Z geometrického významu první derivace víme, že

Z toho plyne, že

Po zderivování podle x dostaneme

Po dosazení (2) a (3) do (1) dostaneme

Výše uvedeným postupem jsme tedy odvodili vzorec pro výpočet zakřivení oblouku v bodě. Nakonec si ještě musíme uvědomit poslední věc:

je-li  y'' > 0, pak je křivka vypuklá; v bodech, kde je y'' < 0, je křivka vydutá.

     V následujícím příkladu si ukážeme použití výše uvedených vztahů.

Příklad 1 (křivost kružnice)

Je dána kružnice o rovnici

Určete křivost kružnice v bodě o x-ové souřadnici 2.

Řešení:

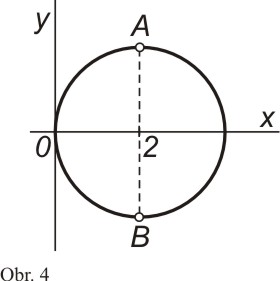Podmínku zadání x = 2 splňují dva body: A = [2; 2], B = [2; -2].

Při řešení je nutno uvažovat, že pro část kružnice pod osou x, je funkce

pro část nad osou x je

Pro část pod kružnicí je tedy

Dále určíme druhou derivaci

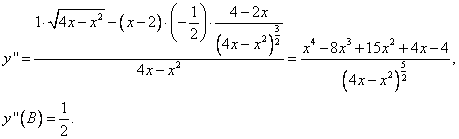
Analogicky bychom určili, že v části kružnice nad osou je

Po dosazení do (4) dostaneme:

Z výše uvedeného výpočtu je vidět, že křivost má v daných bodech stejnou velikost, ale opačné znaménko, což odpovídá situaci na obr. 4: protože se jedná o kružnici, je velikost křivosti konstantní a je rovna 1/R. Rozdílnost znamének je způsobena tím, že vrchní, resp. spodní část polokružnice je vydutá, resp. vypuklá.