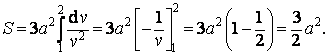[Zpět na stránku matematika křivek]

Obsah plochy opsané křivkou

Příklad 7 (cykloida)

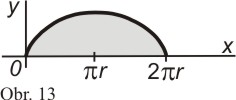
Vypočtěte obsah plochy ohraničené osou x a jedním obloukem cykloidy dané parametricky

Řešení

K řešení použijeme vztahu (10). Nejprve určíme

Potom

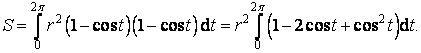
Výraz cos² t upravíme užitím součtového vzorce a dosadíme do výše uvedeného vztahu

Dostaneme

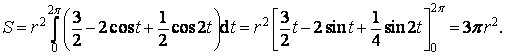
Příklad 8 (Descartův list)

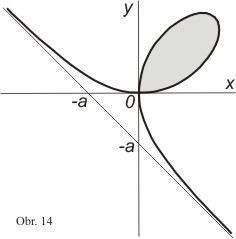
Určete obsah smyčky Descartesova listu, je-li křivka dána rovnicí

Řešení

Rovnici křivky nejprve převedeme na polární tvar

Po dosazení do původní rovnice křivky dostaneme

K řešení úlohy dále použijeme vztah (11). Vezmeme-li v úvahu jen polovinu smyčky, která je symetrická podle přímky y = x, dostaneme pro S vztah

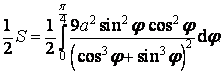
Tento integrál vyřešíme užitím substituce

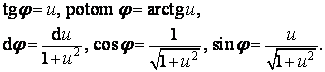
Pak dostaneme (nesmíme samozřejmě zapomenout také na to, že se mění meze)

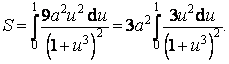
Dále použijeme ještě jednu substituci

Nakonec po dosazení (a změně mezí) dostaneme