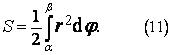[Zpět na stránku matematika křivek]

Obsah oblasti

V této části odvodíme základní vztahy pro výpočet obsahu oblasti pro různé způsoby zadání křivky.

Připomeňme si známý vztah pro výpočet obsahu plochy, je-li křivka dána rovnicí y = f(x). Obsah pod grafem funkce je potom dán vztahem

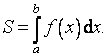
Je-li rovnice křivky dána parametricky ve tvaru

potom můžeme psát

Dále můžeme psát

Obsah plochy pak je dán vztahem

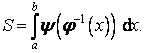
Užitím substituce x = φ(t) dostaneme po derivaci

a po dosazení do vztahu pro S obdržíme

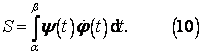
Obsah oblasti  - polární souřadnice

      Nechť r = f(φ) je spojitá funkce na intervalu α ≤ φ ≤ β. Chceme určit obsah oblasti vymezené pod grafem funkce f a polopřímkami φ = α a φ = β. Budeme uvažovat β - α ≤ 2π. Pro jednoduchost budeme předpokládat f ≥ 0.

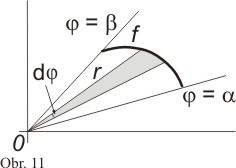
Oblast rozdělíme na malé výseče, které můžeme téměř považovat za trojúhelníky o základně r·dφ a výšce r. Obsah dS jednoho trojúhelníku je dán vztahem

Obsah celé oblasti pak určíme integrací