[Zpět na stránku Matematika křivek]

Elipsa a hyperbola - matematika

Historie

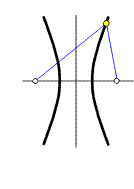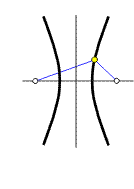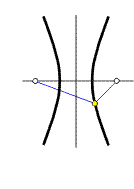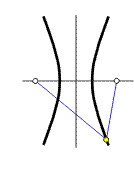
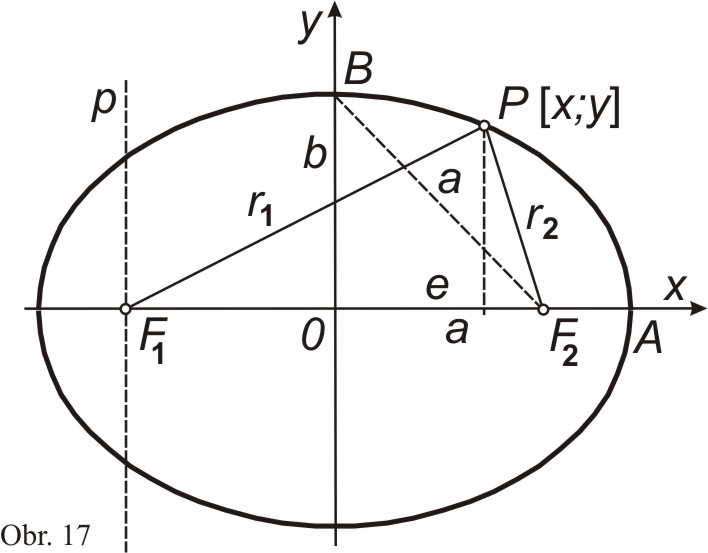
     Elipsa a hyperbola jsou křivky, jejichž body mají konstantní součet, resp. rozdíl svých vzdáleností (průvodiče r₁, r₂) od dvou pevných bodů (ohnisek F₁, F₂) v rovině, tj.

      Konstanta a je u obou křivek polovina součtu, resp. rozdílu průvodičů, nazýváme ji délkou hlavní poloosy křivky
(ale musí u elipsy být 2a > 2e, naopak u hyperboly 2a < 2e).

     Označíme-li vzdálenost ohnisek 2e, pak pro elipsu platí

a pro hyperbolu platí

kde b je délka vedlejší poloosy.

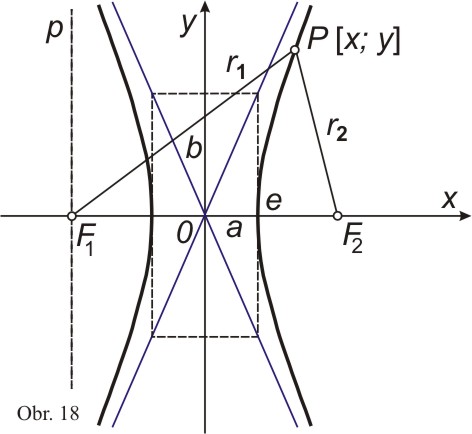Je tedy u elipsy e² = a² - b², u hyperboly e² = a² + b².

pokud bychom vztah

dále upravili, dostaneme osové rovnice elipsy, resp. hyperboly

(Podrobnější odvození je možno nalézt v současných učebnicích matematiky - analytická geometrie.)

Elipsa

Zavedeme-li poměr

je tzv. číselná (numerická) výstřednost (excentricita) elipsy, resp. hyperboly. Pro elipsu je ε > 1, pro hyperbolu je ε < 1. Dále můžeme psát pro průvodiče bodu P na elipse vztah

a tedy

čili

Po dalších úpravách dostaneme

Výraz pro r₁ lze upravit na tvar

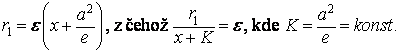
Z toho je vidět, že poměr vzdáleností bodu elipsy od ohniska F₁  a přímky x = K (řídící přímky), je stálý (= ε). Obdobný vztah lze odvodit i pro r₂.

Hyperbola

Pro hyperbolu můžeme psát obdobně

potom

dále platí (pro větev s kladnými x)

a proto

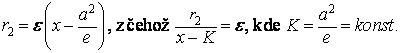
Opět tedy můžeme říci, že poměr vzdáleností bodu hyperboly od ohniska F₂ a přímky x = K (řídící přímky), je stálý (= ε). Obdobně bychom mohli napsat i vztah pro r₁ a druhou větev hyperboly, tj. platí r₂ - r₁ = 2a, atd.

Parametrické rovnice

Elipsu a hyperbolu (v osách souřadnic) je možno vyjádřit parametricky, a to elipsu rovnicemi

a hyperbolu rovnicemi

kde t v tomto případě vyjadřuje úhel průvodiče měřený od osy x proti směru hodinových ručiček.

Speciálním případem elipsy je kružnice, tj. když a = b = r. Potom je e = 0, ε = 0 a platí

nebo parametricky

Speciálním případem hyperboly je rovnoosá hyperbola, tj. když a = b. Potom je

a platí

nebo parametricky