[Zpět na stránku Matematika křivek]

Dioklova kisoida

Historie

Tuto křivku znali již staří Řekové a nazvali ji kisoidou (cissoidou) podle domnělé podobnosti s břečťanovým listem (v části ležící v základní kružnici společně s jeho příslušným obloukem; břečťan se řecky nazýval kissos).

Tuto křivku sestrojil řecký geometr Diokles (250 až 100 let př. n. l.).

Postup, jak je kisoida sestrojena, lze zobecnit.

Modelování

Postup konstrukce kisoidy

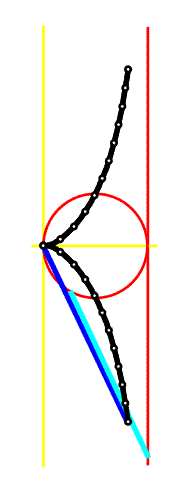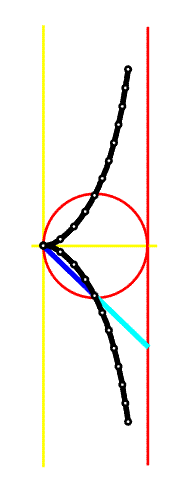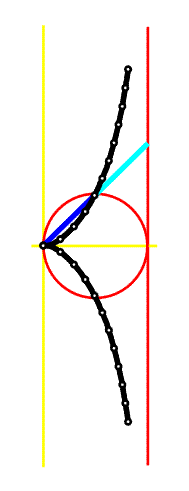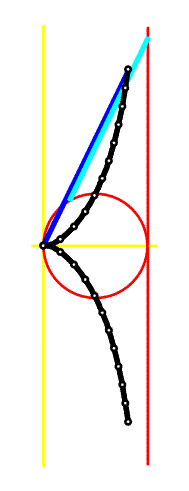
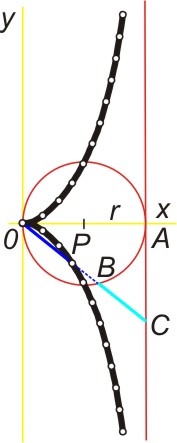
Základní čáry ke konstrukci kisoidy jsou kružnice a její tečna v určitém bodě. V protilehlém místě vzhledem k bodu dotyku A sestrojíme přímku rovnoběžnou se zvolenou tečnou - osu y, za osu x pak zvolíme přímku, jejíž část tvoří spojnice OA (viz obr. vlevo). Z bodu O budeme nanášet paprsky na tečnu a na kružnici dle obr. vlevo a animace. Podstatné na celé konstrukci je, že se musí rovnat délky barevně vyznačených úseček, tj. musí platit, že |OP| = |BC|. Body B pak vytvoří tzv. kisoidu.

Nyní popíšeme výše uvedený postup analyticky. Přímka svazku jdoucího bodem P = [x, y] protíná základní kružnici (o poloměru r) mimo bod  O = [0, 0] v bodě B = [b₁, b₂], který tedy leží na přímce o rovnici

a na kružnici

Dostali jsme soustavu dvou rovnic o dvou neznámých b₁, b₂, jejímž řešením dostaneme

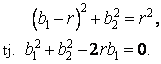
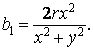
 Přímka procházející bodem P protíná základní tečnu v bodě C. Protože platí  |OP| = |BC|, pak můžeme psát

Po dosazení za b₁ dostaneme

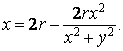
Položíme-li

dostaneme rovnici kisoidy

Z této rovnice vyplývá, že kisoida leží pouze v 1. a 4. kvadrantu, a to v přímém pásu omezeném osou y a přímkou x = a; je souměrná podle osy x. Je to křivka 3. stupně.

V polárních rovnicích lze vyjádřit rovnici kisoidy ve tvaru

Parametrické vyjádření rovnice kisoidy je dáno vztahy