[Zpět na stránku Matematika křivek]

Descartův list

Historie

První zmínka o této křivce se objevuje v Descartových dopisech Mersennovi v roce 1638. Její celkový průběh vyšetřil až Huygens v roce 1692.

Descartes hledal tvar této křivky v 1. kvadrantu a věřil, že tento list také opakovaně nalezne i v ostatních kvadrantech jako tvar čtyř okružních lístků rostlin. Roberval se domníval, že křivka má tvar jasmínu. Jím navržené jméno křivky "fleur de jasmin" bylo později změněno, křivka je často známá pod názvem "noneud de ruban".

Modelování

Matematický popis

Descartův list je kisoida elipsy

vzhledem k přímce

pro pól O. Tato křivka má v kartézských souřadnicích rovnici

v polárních souřadnicích

a v parametrickém vyjádření

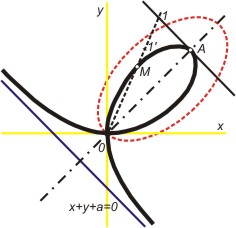
Descartův list je křivka třetího stupně souměrná podle přímky y = x, v bodě O má uzel, s tečnami v osách x, y, v bodě

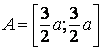
má vrchol; asymptotu má v dané přímce x + y + a = 0.

Konstrukce bodů Descartova listu

1. Pólem O vedená polopřímka protíná tečnu ve vrcholu A v bodě 1.
2. Na této polopřímce určíme bod 1' tak, že |A1| = |A1'|;  potom sestrojíme k bodu 1 vzhledem k O a 1' harmonický bod M 
   (tj. dvojpoměr (O, 1' , 1, M) = -1)).
3. Bod M je bodem Descartova listu.