[Zpět na stránku integrální počet]

Pojem určitý integrál

      (z fyzikálního hlediska)

      Předpokládejme, že jsme nějakým způsobem zjistili, že rychlost tělesa (hmotného bodu) padajícího volným pádem je daná vztahem v = gt. Na základě tohoto vztahu chceme určit závislost dráhy tělesa na čase, tj. funkcí s = s(t). Odpor prostředí nebudeme uvažovat. Teoreticky budeme chtět vlastně odvodit známý vztah

Při dalších úvahách budeme předpokládat, že v čase t = 0 je počáteční rychlost v = 0 a počáteční dráha s = 0. Budeme uvažovat, že těleso začíná padat v čase t = 0.

     Dráha uražená tělesem za dobu dt je rovna ds = v dt, přičemž v = gt.  Celkovou uraženou dráhu pak spočteme jako součet všech elementárních (diferenciálních) drah ds.

     Při zjišťování součtu elementárních drah ds užijeme některé geometrické poznatky.

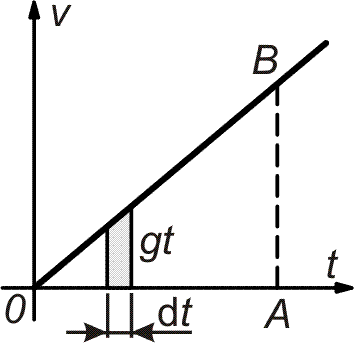
Na obrázku vpravo je zakreslený elementární útvar (lichoběžník, který si pro naše úvahy převedeme na obdélník se střední hodnotou výšky) o ploše dS = gt dt = v dt. Hodnota v dt však z fyzikálního hlediska představuje elementární dráhu ds uraženou tělesem za časový interval dt. Celková uražená dráha za dobu t, potom musí odpovídat ploše všech elementárních útvarů vytvořených nad všemi elementárními úseky v časovém intervalu á0; tñ. Z geometrických představ je zřejmé, že sčítáním všech uvedených elementárních plošek dostaneme plochu trojúhelníka OAB. Pro velikost této plochy S platí Protože to fyzikálně představuje dráhu s uraženou padajícím tělesem, je možno také psát

To, co jsme udělali, je možno také zapsat takto:

Vztah mezi neurčitým a určitým integrálem

Jestliže počítáme neurčitý integrál  z funkce f(x), můžeme psát

F(x) je funkce primitivní k funkci f(x).

Potom pro hodnotu určitého integrálu v mezích od a do b, kterou označujeme symbolem  platí Určitý integrál z funkce f(x) je tedy rozdíl funkčních hodnot funkce F(x) pro příslušné integrační meze.

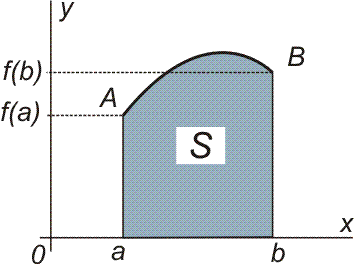Čísla a, b jsou dolní a horní mez. Pravá strana ukazuje, jak se určitý integrál vypočítá: do neurčitého integrálu psaného bez integrační konstanty dosadíme za x nejdříve horní mez, pak dolní, a obě hodnoty v tomto pořadí odečteme. Takto definovaný určitý integrál není tedy funkce, nýbrž číslo.

Vlastnosti určitého integrálu:

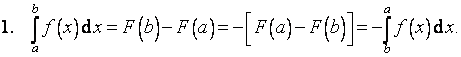
      Výměnou integračních mezí změní určitý integrál jen své znaménko.

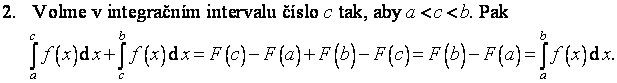
       Integrační interval lze rozdělit na dvě (nebo více) částí (v tom smyslu, že horní mez jedné části je dolní mez druhé části atd.).

Výpočet určitého integrálu substituční metodou:

      Při výpočtech určitých integrálů substituční metodou, která se v praxi a v aplikacích často vyskytuje, je třeba dbát této zásady:

Zavedeme-li novou proměnnou, je nutno přepočítat i meze pro tuto novou proměnnou.