Pojem neurčitý integrál

Jednou z úloh integrálního počtu je studium operace, obrácené k operaci derivování.

Úkolem derivování je určit k dané funkci F(x) její diferenciál dF(x) = f(x)dx, popřípadě derivaci F´(x) = f(x).

Integrální počet si klade za úkol studium obrácené operace. Tato operace se nazývá integrování a jejím úkolem je najít k danému výrazu f(x)dx, pokládanému za diferenciál neznámé funkce F(x), tuto neznámou "primitivní" funkci F(x).

     Primitivní funkcí daného výrazu f(x)dx se nazývá každá funkce F(x), jejíž diferenciál je roven f(x)dx neboli jejíž derivace je rovna dané funkci f(x).

Je tedy mezi výrazem f(x)dx a příslušnou primitivní funkcí vztah

dF(x) = f(x)dx

nebo

F´(x) = f(x).

Přímou operaci - diferencování (resp. derivování) - označujeme písmenem d; symbol

dF(x),

označuje diferenciál funkce F(x).

Obrácenou operaci - integrování - označujeme znakem ∫ , takže symbol

∫f(x)dx

znamená, že na výraz f(x)dx  se provádí operace obrácená k derivování.

Symbol

∫f(x)dx

se nazývá neurčitý integrál a čte se: "neurčitý integrál  f(x)dx".

Např. neurčitý integrál výrazu x³dx se napíše takto:

∫x³dx.

To, že se zavedený symbol nazývá neurčitým integrálem, se vysvětluje mnohoznačností (tj. neurčitostí) řešení, kterou se vyznačuje integrování.

Toto si ukážeme na následujícím příkladu.

Příklad: Mějme systém funkcí Pro všechny tyto funkce je y´ = 3x2, neboť se vzájemně liší konstantním sčítancem, jehož derivace je rovna nule. Tečny všech těchto křivek v bodech, jejichž souřadnice x jsou si rovny svírají s osou Ox stejné úhly. Všechny tyto křivky dostaneme posouváním křivky     y = x3 svislým směrem. To zřejmě platí pro všechny křivky tvaru y = x3 + C, kde C je libovolné číslo (pro první křivku C = 0, pro druhou C = 1, ... , atd.)

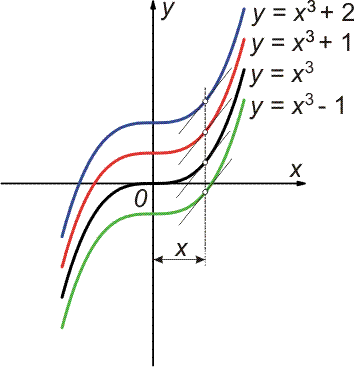   Nyní budeme řešit obrácenou úlohu: k dané derivaci y´ = 3x² určit primitivní funkci. Je zřejmé, že nemůžeme rozhodnout, která z křivek

y = x³ + C

   byla původně dána. Všechny funkce tvaru y = x³ + C, vyjadřující výše uvedené křivky, vyhovují podmínce y´ = 3x². 

         To ale znamená, že úloha najít neurčitý integrál není jednoznačně řešitelná, neboť libovolná funkce tvaru x³ + C, kde C je libovolné číslo, je řešením integrálu

 ∫3x² dx.

Musíme proto psát

∫3x² dx = x³ + C

a uvědomit si, že výsledek x³ + C je zkrácené vyjádření nekonečně mnoha odpovědí, neboť písmeno C může znamenat libovolné číslo.

Protože jsme nenalezli jedinou určitou odpověď, nazývá se sám symbol  ∫3x² dx neurčitý integrál.

Stejný výsledek dostaneme při výpočtu primitivní funkce pro každou funkci f(x).