[Návrat na hlavní stránku]
[Návrat na hlavní stránku]
Užití posloupností ve fyzice

1. Dvě osoby se vydají současně na cestu stejným směrem z míst vzdálených od sebe 60 km. 1. osoba urazí první den 40 km a každý následující den o 3 km méně; 2. osoba pak urazí první den 30 km a každý následující den o 2 km více. Za kolik dní dohoní 2. osoba 1. osobu? Za kolik dní budou od sebe nejvíce vzdáleni a jaká je tato vzdálenost?
Řešení
2. Teploty Země přibývá o 1
0
C na 33 m. Jak velká je teplota na Annenské šachtě v Příbrami, která je 1311 m hluboká, je-li v hloubce 25 m stálá teplota 25
0
C ?
Řešení
3. Jak dlouho by padala koule do hloubky 2500 m - hloubka nejhlubšího dolu na světě v jižní Africe - víte-li, že v první sekundě proběhne dráhu 4,904 m a za každou další sekundu o 9,808 m více?
Řešení
4. Volně padající těleso proběhne za první sekundu dráhu
g
/2 m a za každou následující sekundu dráhu o
g
m větší než za sekundu předcházející. Jakou dráhu vykoná za
t
sekund? (Odpor vzduchu neuvažujte.)
Řešení
5. Rychlost šíření zvuku ve vzduchu při 0
0
C je asi 331 m/s; s rostoucí teplotou roste také rychlost zvuku asi o 0,6 m/s na každý stupeň. Jaká je rychlost šíření zvuku při teplotě 25
0
C ? Při jaké teplotě je rychlost zvuku 340 m/s ?
Řešení
6. Dvě tělesa, která jsou od sebe 48 m vzdálená, se dají současně do pohybu po přímé dráze proti sobě. Jedno proběhne za první sekundu dráhu 4 m a v každé následující sekundě o 2 m více než za sekundu předchozí. Druhé se pohybuje rovnoměrně rychlostí 10 m/s. Za jakou dobu nastane srážka?
Řešení
7. Koule se valí po nakloněné rovině tak, že v první sekundě urazí dráhu
a
metrů, v druhé sekundě
a
+
b
metrů, ve třetí sekundě
a
+ 2
b
metrů atd.
a) Vypočtěte dráhu koule po
n
sekundách. Volte
a
= 0,3 m;
b
= 0,6 m;
n
= 5 s.
b) Vypočtěte, za kolik sekund proběhne koule po nakloněné rovině dldlouhé
L
= 30 m, je-li
a
= 0,3 m;
b
= 0,6 m.
Řešení
8. Při dopadu z výšky
h
na vodorovnou rovinu se odrazí míč jen do 75% této výšky. Do jaké výšky míč vystoupí po pátém odrazu, byl-li na počátku spuštěn z výšky
h
= 2 m?
Řešení
9. V nádobě je
m
gramů radonu. Jaké množství radonu zbyde v nádobě za 36 dní, je-li poločas rozpadu 4 dny? (Za každé 4 dny se rozpadne polovina jeho množství.)
Jaké množství radonu by zbylo v nádobě za 4
t
dny? Seřaďte jednotlivá množství radonu do posloupnosti a vyšetřete ji (
t
= 0, 1, 2, 3, ...).
Řešení
10. Světelný paprsek dopadá pod úhlem
a
na
k
skleněných destiček, které leží na sobě. Tloušťka první destičky je
h
, tloušťky ostatních destiček tvoří
a) aritmetickou řadu o diferenci
d
takové, že
kd
=
h
;
b) geometrickou řadu s kvocientem
q
.
Určete posunutí vystu
pujícího paprsku, je-li index lomu skla
n
. Vypočtěte v případě b) i pro
k
=
¥
.
Návod: pro posunutí
v
paprsku vystupujícího z planparalelní desky tloušťky
h
lze odvodit vztah (můžete se pokusit o jeho odvození, ale tomu nutné znát zákon lomu a vztahy me
zi goniometrickými funkcemi):
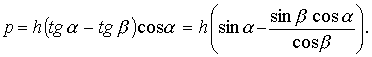
Protože
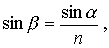
je
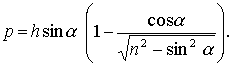
Řešení
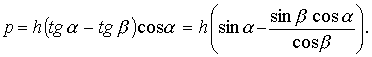
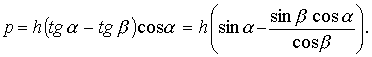
![]()