Předpokládáme, že 2. osoba dohoní první za
x dní. Pohyb 1. osoby je vlastně aritmetická posloupnost s prvním členem a 1 = 40 km a diferencí d a = - 3 km.Pohyb 2. osoby je aritmetická posloupnost s prvním členem
b 1 = 30 km a diferencí d b = 2 km.
V první části úlohy hledáme n = x . Použitím vzorců pro součet prvních n členů aritmetické posloupnosti a s využitím podmínky pro počáteční vzdálenost dostaneme:
![]()
Po úpravách dostaneme kvadratickou rovnici, kterou dále vyřešíme:
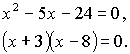
Úloze vyhovuje pouze kladné řešení
x = 8 . 2. osoba dohoní první za 8 dní.
![]()
Tuto rovnici budeme dále upravovat.
Dostaneme:
![]()
což je kvadratická rovnice.
Určíme diskriminant této rovnice:
![]()
Fyzikální význam bude mít pouze kladný kořen
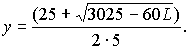
Maximální vzdálenost bude při nulovém diskriminantu
D .Z podmínky D = 0 dostaneme
![]()
Tomu odpovídá
![]()