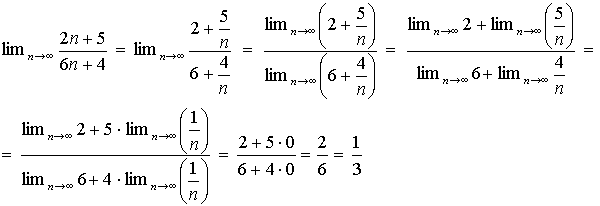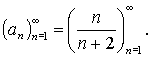
Mějme posloupnost
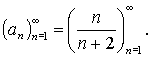
Vypišme prvních patnáct členů této posloupnosti
![]()
Je vidět, že se členy posloupnosti neomezeně blíží číslu 1.
Ne vždy ale tento případ nastane.
1. Jestliže se
s rostoucím n členy posloupnosti a n neomezeně blíží k určitému reálnému číslu a , říkáme o tomto čísle, že je limitou (vlastní limitou) posloupnosti .
2. Jestliže se s rostoucím
n členy posloupnosti a n blíží k + ¥ nebo - ¥ , říkáme, že posloupnost má nevlastní limitu + ¥ nebo - ¥ .
3. Jestliže se s rostoucím
n se členy posloupnosti a n neblíží ani k žádnému číslu a Î R , ani k + ¥ nebo - ¥ , pak říkáme, že posloupnost nemá ani vlastní , ani nevlastní limitu neboli je oscilující .
Definice limity posloupnosti
Reálné číslo
a je limita posloupnosti
![]()
se členy
a n Î R , právě když ke každému (jakkoli malému) číslu e > 0 existuje přirozené číslo n 0 takové,
![]()
Skutečnost, že posloupnost
![]()
má limitu a Î R , se vyjadřuje zápisem
![]()
Posloupnosti, které mají vlastní limitu (
a
Î
R
), se nazývají
konvergentní posloupnosti
.
Posloupnosti, jež nejsou konvergentní, se nazývají
divergentní posloupnosti
(
divergují
k +
¥
nebo -
¥
anebo jsou
oscilující
).
V matematice se z této definice odvozuje řada limit. V praxi se to ale provede tak, že se z této definice odvodí věty o limitách a z těch se pak vychází při praktickém výpočtu.
Věty o limitách posloupností
1. Každá posloupnost má nejvýše jednu limitu. (Tedy buď vlastní limitu nemá, anebo má právě jednu.)
2. Každá konvergentní posloupnost je omezená.
3. Každá monotónní omezená posloupnost je konvergentní.
Dále použijeme zkrácený zápis
![]()
5. Věta o limitě součtu, rozdílu, součinu a podílu posloupností.
Nechť posloupnosti a n , b n jsou konvergentní a c je libovolné reálné číslo. Pak jsou konvergentní i posloupnosti ( a n + b n ), ( a n - b n ), ( a n × b n ). Je-li navíc
![]()
je konvergentní také posloupnost
![]()
a platí
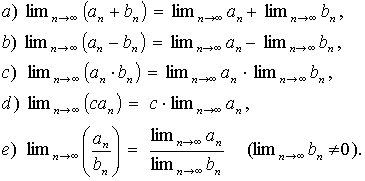
Užitečné - v praxi často používané limity:
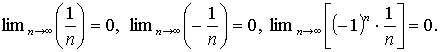
Příklad - užití výše popsaných poznatků pro výpočet limity posloupnosti: