 Zlatá
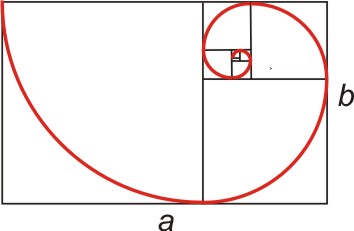
spirála je taková spirála, kterou lze vepsat do tzv. zlatého obdélníku.
Zlatá
spirála je taková spirála, kterou lze vepsat do tzv. zlatého obdélníku.
Do tohoto obdélníku vepíšeme ke kratší straně b čtverec o straně b, zbylá plocha je opět zlatý obdélník, do něj opět stejným postupem vepíšeme další čtverec, atd. Do takto zkonstruovaného čtverce vepíšeme čtvrtkružnici -tím získáme logaritmickou spirálu.
Zlatý obdélník - obdélník, jehož strany jsou ve stejném poměru. Je-li a > b, pak ve zlatém obdélníku musí platit
![]()
Z této rovnice je možno následujícím odvodit číselnou hodnotu poměru a/b. Výše uvedenou rovnici přepíšeme na tvar
![]()
a řešíme jako kvadratickou rovnici v proměnné a. Rovnici vyhovuje pouze kladný kořen, a proto dostaneme
![]()
Chceme-li nyní odvodit příslušnou rovnici výše popsané logaritmické spirály, vyjdeme ze vztahu
![]()
Položíme r/c = a/b , což platí pro φ = π/2 a zlogaritmujeme.
Potom dostaneme
![]()
Po dosazení za φ = π/2 a vyjádření k dostaneme
![]()
Rovnici zlaté spirály pak můžeme psát např. ve tvaru
![]()