Hyperbolická spirála
Historie
Hyperbolickou spirálu navrhl Piere Varignon v roce 1704. Dále jí pak studoval Johann Bernoulli v letech 1710 - 1713 a též Cotes v r. 1722. Piere Varignon byl profesorem matematiky na Collège Mazarin a později na Collège Royal.
Matematický popis
Hyperbolická
spirála je inverzní k Archimédově spirále, tj. má v polárních souřadnicích
rovnici
Bude-li se úhel φ blížit k nule, průvodič neomezeně poroste. Pro φ = π je r0 = a/φ, pro φ = 2π je průvodič poloviční (r = a/(2π) = r0/2); pro φ = 3π je r = r0/3 atd.
Při neomezeném vzrůstu úhlu φ se hodnoty průvodiče blíží k nule, ale nikdy jí nedosáhnou. To znamená, že křivka se neomezeně blíží k pólu O, ovinuje se kolem pólu, ale nikdy ho nedosáhne. Takový bod nazýváme asymptotickým bodem křivky.
Konstrukce hyperbolické spirály
Abychom sestrojili graf křivky, přepíšeme její rovnici na tvar
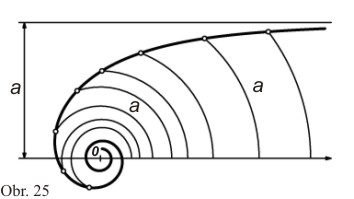
Ze skutečnosti, že rφ = konst. , vyplývá níže uvedený postup konstrukce spirály. Sestrojíme řadu soustředných kružnic se středem v pólu a na každou kružnici naneseme od jejího průsečíku s polární osou oblouk délky a. Délka každého oblouku se rovná součinu příslušného úhlu φ s poloměrem r kružnice, tj. rφ; krajní bod každého oblouku, který tak obdržíme, tedy bude bod, který náleží spirále (obr. 25).
V závislosti na tom, jak se bod spirály vzdaluje od pólu, se poloměry kružnice zvětšují, oblouk se neustále "narovnává" a blíží se tvaru úsečky, která je kolmá k polární ose. To ukazuje, že body spirály se při přibližování úhlu φ k O blíží k přímce, která je rovnoběžná s polární osou a prochází od ní ve vzdálenosti a. Vzdálenost bodů spirály od této přímky se stále zmenšuje, nikdy však nepřejde v nulu. V tomto případě říkáme, že se spirála asymptoticky blíží ke zmíněné přímce.
Pro záporné hodnoty úhlu φ bychom dostali spirálu, která je souměrná s právě vyšetřovanou podle přímky procházející pólem kolmo k polární ose.
Pokud bychom chtěli znázornit hyperbolickou spirálu graficky pomocí počítače, je výhodné přejít k vyjádření parametrickému, tj.
