Traktrix
Historie
Tuto křivku studoval Huygens v roce 1692, později také Leibniz, Johann Bernoulli, Liouvile a Beltram. Traktrix je často také nazýván jako ekvitangenciální křivka nebo také "tractory".
Matematický popis
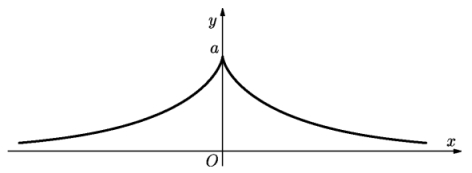Hmotný
bod na konci neroztažitelného přímého vlákna konstantní délky a
opisuje křivku zvanou traktrix, jestliže se druhý krajní konec vlákna
pohybuje po přímce y = 0 a vlákno se zároveň bez skluzu otáčí (obr.).
Tečna každého bodu této křivky, tj. úsek tečny mezi bodem dotyku a jejím
průsečíkem s osou x, má konstantní délku a.
Traktrix je evolventou řetězovky, tj. při kotálení tečny po řetězovce vytváří vrchol řetězovky traktrix.
Parametrické rovnice traktrix (v 1. kvadrantu) jsou dány vztahy
Parametr t vyjadřuje velikost úhlu, který tečna svírá s osou x.
V kartézské soustavě souřadnic je rovnice traktrix (v 1. kvadrantu) dána vztahem (26), tj.
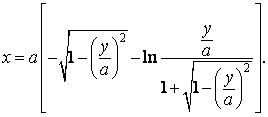
Asymptota traktrix je y = 0.
Příklad
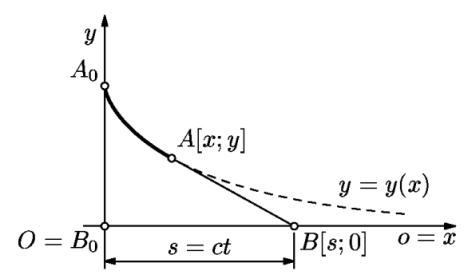Vlečeme-li
tělísko A na laně stálé délky a (obr.) tak, že se bod B
pohybuje rovnoměrně po přímce o, opíše bod A křivku, kterou
nazýváme traktrix. Na základě zadání odvoďte rovnice této křivky.