[Zpět na stránku Matematika křivek]

Klotoida

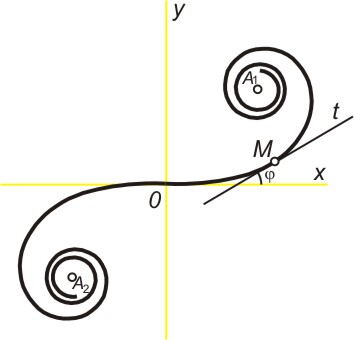
Klotoida je křivka, jejíž poloměr křivosti R v bodě M je nepřímo úměrný délce s oblouku mezi tímto bodem a pevně zvoleným bodem O, tedy platí

     Parametrické rovnice klotoidy s obloukem s jako parametrem jsou dány Fresnelovými integrály

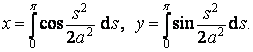
Je-li parametrem úhel

tečny v uvažovaném bodě, mají rovnice tvar

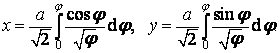
Jestliže

mají parametrické rovnice tvar

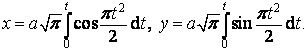
Vlastnosti klotoidy

• Klotoida je symetrická podle bodu O, který je jejím inflexním bodem, a dotýká se v něm osy x.
• Asymptotické body klotoidy jsou body

• Tečny klotoidy jsou rovnoběžné s osou x v bodech, pro které

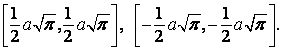
          a jsou rovnoběžné s osou y v bodech, pro které

• Úhel φ křivky s osou x je dán vztahem

• Pro hodnoty a, s, R, φ (v obloukové míře) platí vztahy

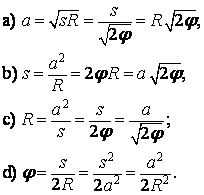
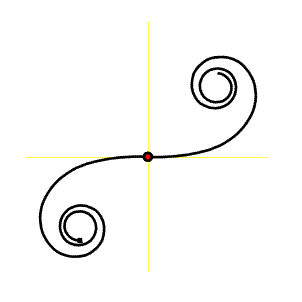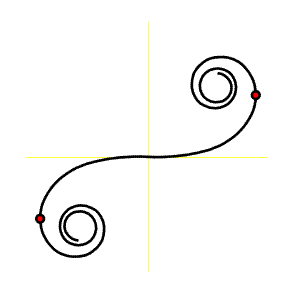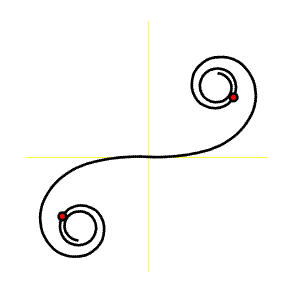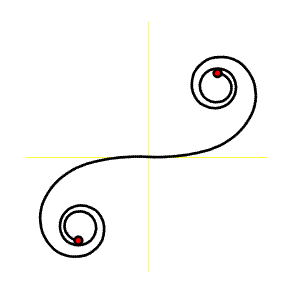
Poznámka

Pro praktické použití jsou Fresnelovy integrály tabelovány. Konstanta a je tzv. parametr, který určuje poměrnou velikost křivky. Je-li např. a = 100, pak pro tuto klotoidu jsou všechny délkové hodnoty pětinásobkem hodnot pro parametr a = 20.

Za porovnání stojí dvojice křivek klotoida - Cornuova spirála (již Euler považoval klotoidu a Cornuovu spirálu za jednu a tutéž křivku lišící se pouze svým názvem).

Praktické užití klotoidy

Zde je uvedena část textu přednášky na VUT BRNO ( http://www.fce.vutbr.cz/PKO/0M2/PREDN2/predn2.htm):

"Graf křivosti směrového motivu tečna – kružnice – tečna je nevýhodný. V bodě dotyku vzniká tzv. „příčný ráz“, za předpokladu, že vozidlo je pevně vedeno (proto je příčný ráz známý u kolejových vozidel, pokud je oblouk bez přechodnice nebo je špatně provedený). Silniční vozidla nejsou pevně vedená, příčný ráz u nich nevzniká, ale je to za tu cenu, že se mohou odchylovat od dráhy určené vytyčenou naprojektovanou křivkou. pokud by vozidlo mělo dodržet trajektorii tečna – kružnice – tečna, musel by řidič při konstantní nenulové rychlosti nastavit poloměr dráhy na požadovanou kružnici (otočit volantem do konečné polohy) za nulový čas. To není možné. Jinou možností je změnit v bodě dotyku rychlost na nulovou, nastavit poloměr a pokračovat v jízdě. To není rozumné a užitečné.

Běžný způsob řešení tohoto rozporu je odchýlit se trajektorií od vytyčené dráhy. Při malých odchylkách to neznamená nic nebezpečného, při velikých (v závislosti na poloměru, rychlosti, rychlosti změny křivosti, šířce jízdního pruhu) to může vést ke kolizi s vozidly v jiném pruhu nebo k vyjetí mimo vozovku). Zásadní způsob, jak se vypořádat s tímto problémem je použít oblouk s přechodnicí.

Přechodnice je křivka, která plynule mění svou křivost. V optimálním případě je její křivost na konci a na začátku shodná s křivostí směrového prvku, na který navazuje (u kružnicových oblouků s přechodnicemi je to nulová křivost na začátku v místě připojení na přímku a křivost o velikosti 1/R na konci v místě připojení na kružnici).

V silničním stavitelství se běžně používá jako přechodnice klotoida."

Více informací o této problematice je možno obdržet na http://www.fce.vutbr.cz/PKO/0M2/PREDN2/predn2.htm.