★ Back to Table of Contents

Seashell

Seashells are a showcasing of spirals. There are great variety of spiral shapes. Suppose we start with a circle winding around a spiral.

• The circle can change size periodically, creating a corrugated shell somewhat emulate that of Paper Nautilus 04180001m-s.jpg

• If instead of a circle we have a polygon, we can simulate that of top shells 04020013m-s.jpg painted_top-s.jpg or Thather shell. thatcher-s.jpg or cones 09140046m-s.jpg DSCN0180m-s.jpg

• if the rounding shape periodically changes shape, as to become a star, then we might emulate shells that have horns such as the angaria_delphinula angaria_delphinula-s.jpg pink-mouthed murex 09130071m-s.jpg Venus's Comb 09130032m-s.jpg • the periodic change might also emulate those shell having ribs such as the wentletrap angulate_wentletrap-s.jpg the Harper shell 04170013m-s.jpg

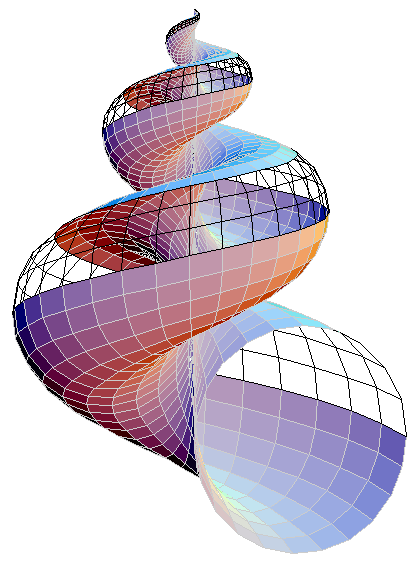
This particular image is generated by the parametric formula:

x = 2*(1 - E^(u/(6*Pi)))*Cos[u]*Cos[v/2]^2,
y = 2*(-1 + E^(u/(6*Pi)))*Cos[v/2]^2*Sin[u],
z = 1 - E^(u/(3*Pi)) - Sin[v] + E^(u/(6*Pi))*Sin[v]}

Graphics code; seashell_wentletrap.nb; shell_para.gcf; shell_para2.gcf; shell_para3.gcf; spindle.gcf corrugated-shell.gcf seashell-tops.gcf seashell-wentletrap.gcf

I offer $5 for anyone who can come up with a parametric formula for the thatcher shell, wentletrap, or Venu's Comb including varios types of murexs that have radiating horns. (Mike Willams has sent me various formulas, see here :20050120-mike_williams.txt

This photo i took with my camera on 2002. The snail is picked up from the street in Bay Area California USA.

Tech name: angaria delphinula, of the Delphinula group. Notice the exquisite color and regular horns.	This type of shell is called wentletrap. The word is originated in German meaning spiral staircase. The characteristics are the creamy white ribs. †
This one is called rose-branched murex. It has the typical shape of murexes. ‡	Lataixis Mawae. A beauty of bizarreness. ‡
This one is caled painted top, of commonedly called “top” shells because they resembel the toy top. Top shells are characterized by a geometrical flat circular cone. †	Zebra Auger. Auger shells are long and thing. ‡
A thatcher shell. How extremely elegant. ＊	This one is called Spider Scorpian shell, of the family commonly called Spider Conch Shells. The spider family are characterized by the feet-like horny projections on their opening. One thing special about spider scorpian conch is that it has beautiful purplish openings. Here's a photo of it's spiral.
These types of shells are called Miter shells, and this is a typical shape. An auger shell are pretty much the same shape but 2 or 3 times longer. ‡	This is a Salisbury's Spindle, of the spindle shell family. One can see that spindle shells are spindle-like.
Lamp Chank ＊	Episcopal Miter ＊
Cowie shells are characterized by their shiny and beautifully patterned surface. Their spiral is not apparent if viewed from the outside. ＊	Grove snail †

The biological classification:

Kindom
 Phylum
  Class
   Order
    Family
     Genus
      Species

The shells animals are of Kindom Animalia (that is, animals), and Phylum Mollusca (they are mollusks). Mollusks have two major class: Gastropoda (gastropods) and Bivalvia (bivalves). Gastropods are those with spiral shells. Snails slugs limpets and abalone are all gastropods. Bivalves are those clam-like shells, including mussell, cockle, clam, oyster.

a Photo Exhibition of Seashells

‡ Photo from Encyclopedia of Shells, by Kenneth R. Wye, 1991. amazon.com↗.

† Photo from National Audubon Society Field Guide to North American Seashells, by Harald A. Rehder. 1981. amazon.com↗.

＊ Photo from a big art book.

• The Algorithmic Beauty of Sea Shells. by Hans Meinhardt, Przemyslaw Prusinkiewicz, Deborah R. Fowler. amazon.com↗

Here's a collection of Seashell icons made in 2001 by Kate England kate.html

★ Back to Table of Contents

Content updated: 2003-05
Last modified: 2003-05
© 1995-97 by Xah Lee. (xah@xahlee.org)
http://xahlee.org/SpecialPlaneCurves_dir/specialPlaneCurves.html