[Zpět na stránku Matematika křivek]

Cykloidy - parametrické rovnice

Prostá cykloida

     Bod kružnice, která se bez skluzu kotálí po přímce, opisuje prostou cykloidu.

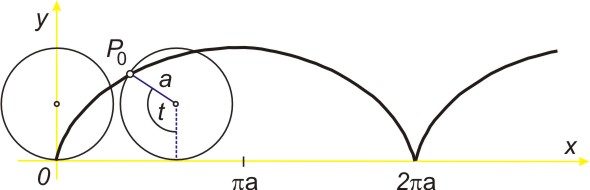
Parametrické rovnice prosté cykloidy (t Î R) jsou dány vztahy

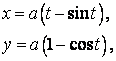
kde a je poloměr kružnice, t je velikost úhlu odvalení.

Délka oblouku OP₀ je dána vztahem

Délka větve:  s = 8a.

Obsah plochy ohraničené jednou větví prosté cykloidy a osou x:   S = 3πa².

Zkrácená cykloida

     Zkrácená cykloida vznikne, jestliže tvořící bod pevně spojený s kotálející se (hybnou) kružnicí leží ve vnitřní oblasti této kružnice ve vzdálenosti d (d < a) od středu kružnice o poloměru a.

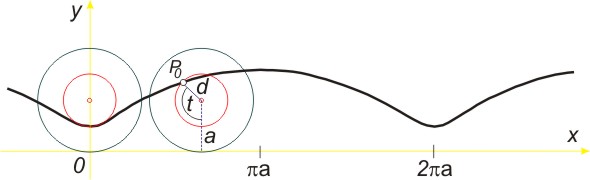
Parametrické rovnice zkrácené  cykloidy      (t Î R) jsou dány vztahy

Prodloužená cykloida

     Prodloužená cykloida vznikne, jestliže tvořící bod pevně spojený s kotálející se (hybnou) kružnicí leží ve vnější oblasti této kružnice ve vzdálenosti d (d > a) od středu kružnice o poloměru a.

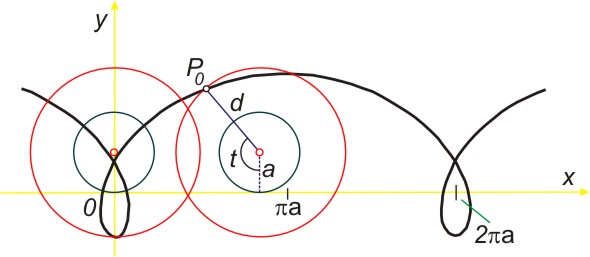
Parametrické rovnice prodloužené  cykloidy    (t Î R) jsou dány vztahy