[Zpět na stránku Matematika křivek]

Cykloidální pohyby - příklady z technické praxe

Příklad  - elipsa

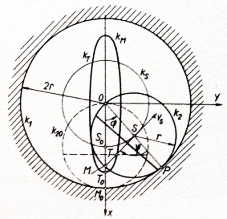
Po vnitřním obvodu kruhového otvoru k₁ se valí kotouč k₂ polovičního průměru; rychlost v_s středu S je stálá - obr.. Určete rovnici trajektorie pohybu těžiště T nevývažku umístěného na kotouči k₂.

Zadáno je: r, v_s = c, |ST| = e.

Řešení

Zavedeme souřadnicový systém Oxy podle obrázku. Za parametr zvolíme úhel φ.

Trajektorie pohybu bodu T

Z rovnosti oblouků

plyne

a parametrické rovnice dráhy

Vyloučíme z výše uvedených rovnic parametr, dostaneme

Trajektorie pohybu všech bodů roviny kotouče k₂ jsou elipsy a trajektoriemi bodů kružnice k₂ jsou průměry kružnice k₁. Pro bod M to plyne z parametrického vyjádření pohybu T, protože e = r.

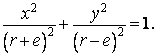
Steinerova cykloida

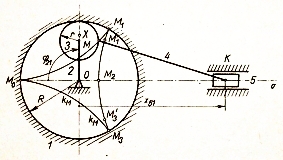
K planetovému mechanismu tvořenému členy 1, 2, 3 s poměrem r : R = 1 : 3 je v bodě M planety připojena binární skupina 4, 5 (viz obr. vlevo). Klika 2 je hnací, smýkadlo 5 pracovní člen. Zvolíme-li délku MK táhla 4 rovnou poloměru křivosti trajektorie k_M v bodě M₂, dostaneme mechanismus s přibližnou klidovou polohou smýkadla v okolí polohy M₂.

Trajektorií bodu M je známá Steinerova cykloida.

Wankelův motor

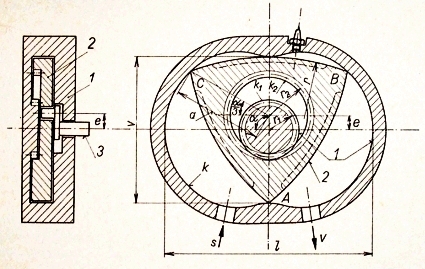Mechanismus Wankelova motoru

Wankelův motor (obr. vlevo) patří k motorům s krouživým pístem.

Píst 2 je tvořen obloukovým rovnoramenným trojúhelníkem ABC (s vybráním). Ten koná pericykloidální pohyb s polodiemi k₂ a k₁ o poloměrech r₂ : r₁ = 3 : 2.

Spalovací komora je válcová, její vnitřní obrys k je dán trajektoriemi vrcholů pístu. Píst pohání kliku 3 o poloměru e; s je sací, v výfukový kanál.