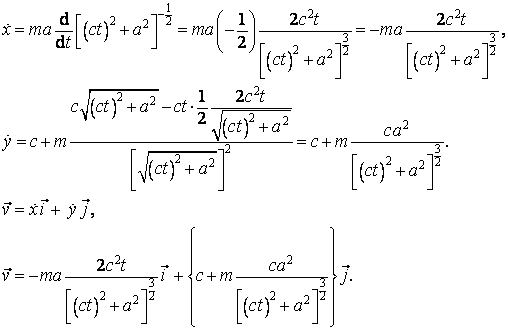Nikomédova konchoida
Historie
Nikomédes byl geometr, který žil v období asi 180 let př. n. l. Jeho
objevení konchoidy bylo připsáno Pappovi. V 17. století ale
matematici zjistili, že Nikomédes použil konchoidu k trisekci úhlu.
Nikomédova konchoida znamenala pokrok při řešení klasického problému, jak
zdvojnásobit krychlový oltář v Delfské věštírně. Stejně tak lze rozdělit
pomocí konchoidy úhel na tři stejné díly.
Pappos (3. stol.) původně křivku pravěpodobně
nazval kochloida (kochlei - v Řecku druh
ryby). Teprve později (5. stol.) ji Proklas přejmenoval na
konchoida
(tvar škeble). Nikomédes (2. stol. př. n. l.) tuto křivku sestrojil
zvláštním přístrojem, který vynalezl.
Parametrické rovnice
Nikomédovy konchoidy jsou dány vztahy
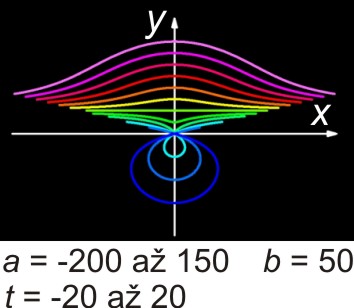
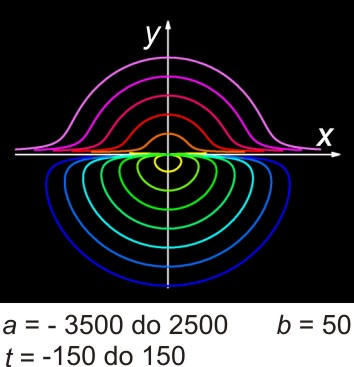
Podle hodnot konstant a, b a parametru t může mít Nikomédova konchoida různé tvary, jak je vidět na níže uvedených obrázcích.
Modelování (pro případ obrázku vlevo) Modelování (pro případ obrázku vpravo - nastaveno jiné měřítko)
Konstrukce Nikomédovy konchoidy
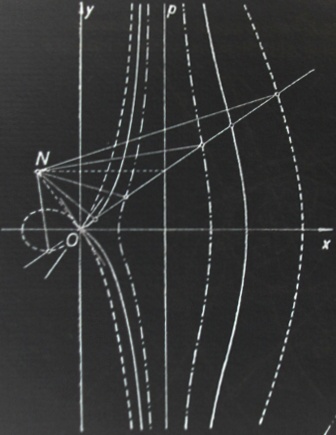
Pevnou přímku x = a protneme svazkem přímek o vrcholu (pólu) O. Od průsečíku přímky s pevnou přímkou naneseme na obě strany úsečky konstantní délky b. Krajní body úseček leží na Nikomédově konchoidě, která má v polárních souřadnicích rovnici
v pravoúhlých souřadnicích
Nikomédova konchoida se skládá ze dvou větví, je souměrná podle osy x, v přímce x = a má asymptotu. Je-li b > a, má jedna větev v O uzel, pro b = a má v něm bod vratu, pro b < a je O izolovaný bod.
Normála všech konchoid, které jsou vytvořeny body zvoleného průvodiče, procházejí týmž bodem N, který je průsečíkem kolmice sestrojené v pólu O k průvodiči a kolmice v průsečíku P průvodiče s přímkou x = a na tuto přímku.
Dnes se pod pojmem konchoidy rozumí obecnější křivky, které lze obdržet zmenšením nebo zvětšením průvodiče každého bodu dané křivky nejen přímky jako je tomu u Nikomédovy konchoidy.
Příklad
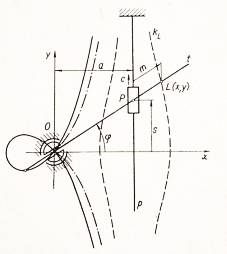Tyč
t (obr.), stále prochází bodem O a její bod P je veden stálou
rychlostí c v drážce p. Vypočtěte průběh rychlosti bodu L
tyče.
Řešení
Vyjdeme z rovnice trajektorie.
Zvolíme souřadnicový systém Oxy tak, aby y || p.
Nyní můžeme napsat rovnici trajektorie pohybu:
kde
Dle obrázku můžeme psát
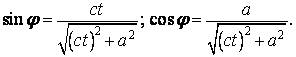
Po dosazení do vztahu pro x a y dostaneme
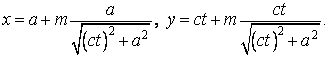
Výpočet okamžité rychlosti z trajektorie pohybu určíme pomocí derivace, tj.
