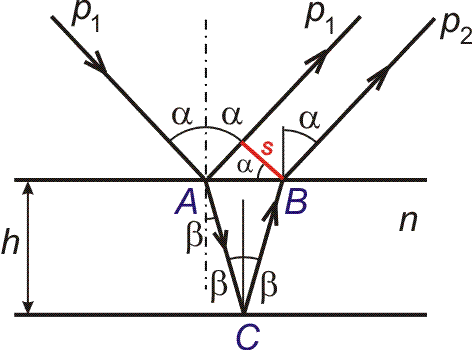
Řešení příkladu č. 9
| Dopadne-li paprsek na první rozhraní v bodu A,
na druhé v bodu C a zpět na první v bodě B, je vzdálenost
paprsku p2 od p1 rovna s =
|AB| cosa.
Označíme-li β úhel lomu, plyne z
trojúhelníku ABC vztah |AB| = 2d
tg β. Dalšími úpravami dostaneme
|
 |
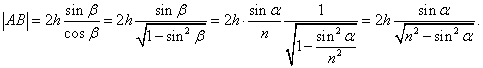
Je tedy vzdálenost s:
![]()
K určení maxima najdeme derivaci funkce s:
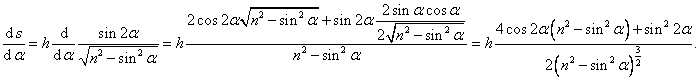
Položíme
![]()
pak musí platit
![]()
po úpravě
![]()
(Při úpravě jsme použili součtové vzorce pro sin 2α = 2 sinα cosα, cos 2α = cos2 α - sin2 α.)
Označíme-li x = sin2 α , pak dostaneme kvadratickou rovnici
![]()
Po vyřešení této kvadratické rovnice a zpětným dosazením za sin α dostaneme řešení
![]()
kde jsme vzali v úvahu n > 1 (ostatní řešení nevyhovují).
Největší vzdálenost paprsků p1 a p2 je pro úhel α, který je dán vztahem
![]()