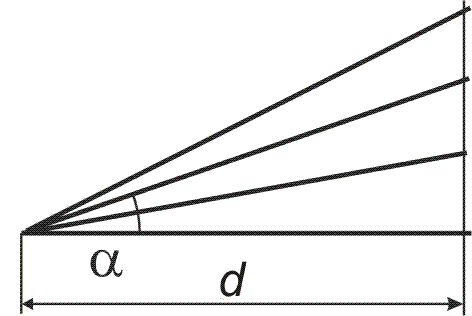
Řešení příkladu č. 5

Pro zrychlení tělesa při pohybu směrem dolů na nakloněné rovině platí vztah Pro pohyb rovnoměrně zrychlený s nulovou počáteční rychlostí platí

kde s je uražená dráha, v tomto případě je to délka nakloněné roviny. Dle obrázku také platí

a)  Po dosazení do vztahu pro s dostaneme

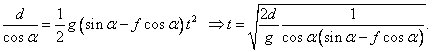
   Pro dané hodnoty t = 0,58 s.

b)  Určíme, pro jaké a bude výraz

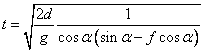
     minimální.

Výraz pro t bude minimální, bude-li

maximální. Toto zjistíme pomocí diferenciálního počtu. Určíme

Z podmínky

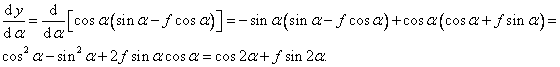
dostáváme

Pomocí druhé derivace určíme, zda tato podmínka určuje lokální maximum:

Po dosazení

dostaneme

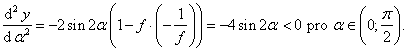
Podmínka

určuje lokální maximum funkce y.

Pro dané hodnoty: a = 55⁰ 54´, tomu odpovídá doba t_min = 0,55 s.