Ve svislém směru platí
![]()
ve vodorovném směru platí
![]()
tak, jak je znázorněno na obrázku vpravo.
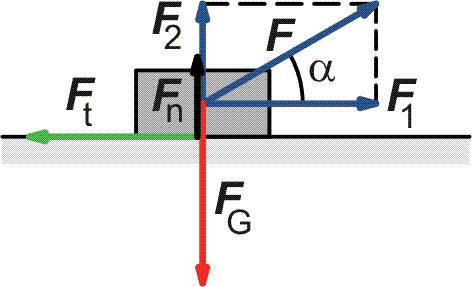
Řešení příkladu č. 2
| Protože se těleso pohybuje rovnoměrně, musí být
výslednice sil na něj působících rovna nule.
Ve svislém směru platí
ve vodorovném směru platí
tak, jak je znázorněno na obrázku vpravo. |
 |
Výše uvedené rovnice můžeme dále rozepsat užitím dříve známých vztahů:
![]()
Za Fn dosadíme do první rovnice, dále ještě dosadíme za FG = mg. Dostaneme
![]()
Pro jaký úhel a bude mít síla F nejmenší velikost určíme pomocí diferenciálního počtu:
![]()
Položíme
![]()
z čehož dostaneme podmínku:
![]()
Pomocí druhé derivace (proveďte sami) dostaneme
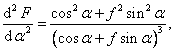
po dosazení podmínky
![]()
bychom zjistili, že pro
![]()
je
![]()
Síla F bude mít nejmenší velikost, bude-li platit tg a = f.
Nyní nám zbývá určit velikost této minimální síly Fmin . Dosadíme do vypočteného vztahu pro F:
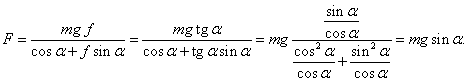
Nyní ještě zpětně dosadíme tak, abychom dostali výsledek vyjádřený pomocí f :
![]()
Po dosazení do vztahu pro F dostaneme:
![]()