Řešení příkladu č. 11

Pro osvětlení  na střední kružnici (na obrázku vpravo je její průmět označen jako bod A) platí vztah po dosazení z obrázku Úlohu je možno řešit dále dvěma způsoby, ukážeme si oba, sami posuďte, který je výhodnější pro tuto úlohu.

1. způsob

Výraz pro E upravíme tak, aby obsahoval úhel α. Platí

Potom

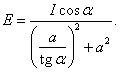
Tento výraz budeme dále upravovat

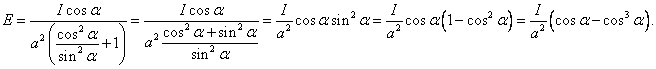
Budeme hledat lokální maximum výrazu pro E:

Položíme

Úhel α budeme hledat v intervalu (0; 90⁰).

Kdyby α = 0 (kolmý dopad), pak by světlo vůbec nedopadlo na vozovku. Toto řešení tedy nevyhovuje požadavkům úlohy.

Musí tedy být

Chceme-li získat výraz pro tg α, pak musíme dále upravit výraz pro tg α takto:

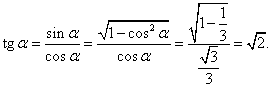
Pro x potom dostaneme

Pro takto vypočtenou výšku x by měl nastat lokální extrém. Vyšetříme, zda je to lokální maximum nebo minimum.

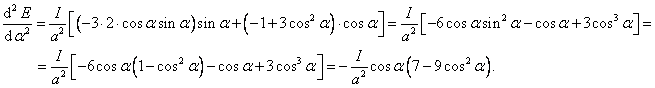
Po dosazení za

dostaneme

Aby vozovka byla co nejvíce osvětlena, musí mít stožár výšku

2. způsob

Výraz pro E upravíme tak, aby obsahoval proměnnou x. Platí

Tento vztah dosadíme do výrazu pro E. Potom

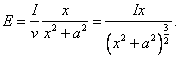
Nyní budeme hledat maximum výše uvedeného výrazu:

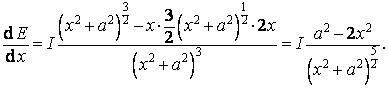
Položíme

Pak

(Úloze vyhovuje pouze kladné řešení.)

Pro takto vypočtenou výšku by měl nastat lokální extrém. Vyšetříme, zda je to lokální maximum nebo minimum.

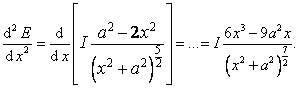
Po dosazení za

do druhé derivace dostaneme

Aby vozovka byla co nejvíce osvětlena, musí mít stožár výšku

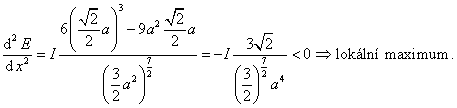
Oba způsoby dávají stejný výsledek. Z uvedeného příkladu vidíme, že postup výpočtu úlohy nemusí být vždy jednoznačný, ale musí vést ke stejnému výsledku.