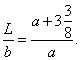
Dále pak můžeme psát
![]()
Pak můžeme psát
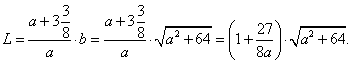
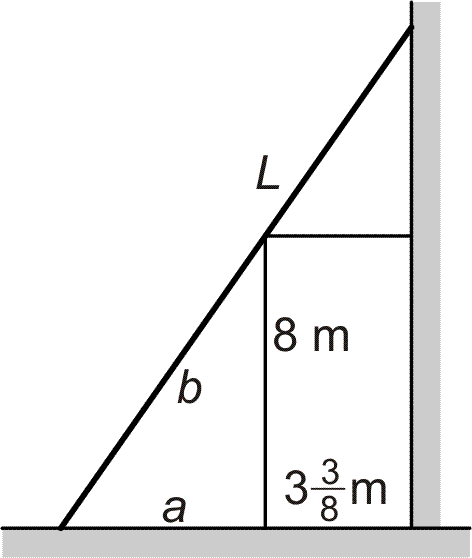
Řešení příkladu č. 7
| Z podobnosti trojúhelníků plyne, že
Dále pak můžeme psát
Pak můžeme psát
|
 |
Nyní budeme hledat lokální minimum funkce L = L(a).
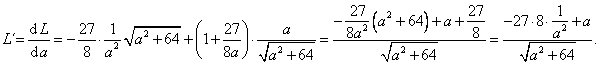
Položíme L´ = 0. Pak obdržíme
![]()
O tom, že se jedná o lokální minimum, bychom se mohli přesvědčit pomocí druhé derivace, ale v tomto případě by výpočet byl dost pracný. Použijeme metodu zjišťování funkčních hodnot nejbližšího okolí bodu a = 6.
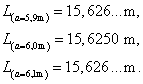
Pro a = 6,0 m nastává lokální minimum, tomu odpovídá minimální délka žebříku L = 15,625 m.