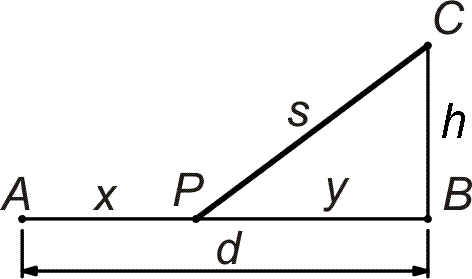
- Označme x, y a s vzdálenosti na obrázku vpravo.
- Cena v miliónech Kč je c = 4x + 5s.
- Vztahy mezi x a y jsou:
![]()
Všechny proměnné můžeme vyjádřit pomocí x nebo y nebo s.
Řešení příkladu č. 2
Hledáme extrém na uzavřeném intervalu! Musíme tedy vyšetřit body nulové derivace a krajní body intervalu.
Všechny proměnné můžeme vyjádřit pomocí x nebo y nebo s.
|
 |
4. Asi nejjednodušší se jeví vyjádřit c pomocí y:
![]()
Matematický problém nyní je: najít minimální hodnotu c na intervalu 0 £ y £ 10. Po zderivování c podle y dostaneme
![]()
Položíme-li c´ = 0, dostaneme
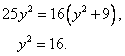
Dostaneme dva kořeny y = - 4 a y = 4, úloze vyhovuje pouze kořen y = 4.
Vypočteme c v bodech y = 0, 4, 10.
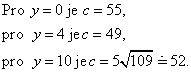
Tento výpočet funkčních hodnot v krajních bodech intervalu nám nahrazuje použití druhé derivace při vyšetřování extrému.
Minimální cena je tedy 49 miliónů Kč a dosáhne se jí při y = 4, tedy umístěním křižovatky 4 km západně od B (6 km východně od A). Tím se ušetří víc než dva milióny Kč proti přímé cestě a víc než 5 miliónů Kč proti cestě ve tvaru L s úhlem v B.