Podstata této metody spočívá v tom, že při výpočtu integrálu ∫f(x)dx zavedeme novou proměnnou t místo x, vázanou s x rovnicí x = φ(t) tak, aby se integrovaný výraz zjednodušil. Přitom se daný integrál ∫f(x)dx převede na integrál
![]()
Tak dostáváme vztah
![]()
(v tomto vztahu předpokládáme všechny funkce spojité).
Příklad užití substituční metody:
Vypočtěte integrál
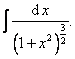
Řešení
Položíme
![]()
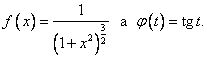
Je tedy
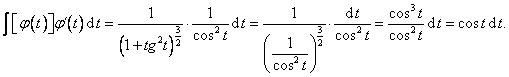
Dále můžeme tedy psát
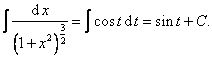
Tento výsledek ale musíme vyjádřit pomocí původní proměnné x. Protože x = tg t, je nutno vyjádřit sin t pomocí tg t a pak zaměnit tg t za x.Postupně dostaneme
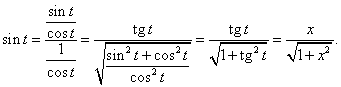
Nakonec
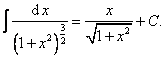
Další příklady na integraci substitucí jsou uvedeny ve Cvičení 4.